http://akimpotos.blogspot.jp/2012/12/2-triplets-paradox-2-deterministic.html
今までの纏め Summary
ローレンツ変換はある系への座標変換です。
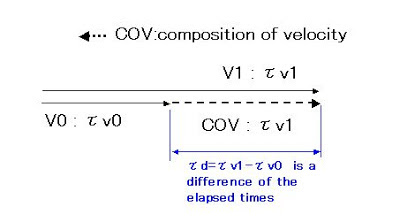
速度の変換という面では合成速度を算出します。
経過時間の差は固有時間を使用して算出できます。
つまり、同時に進行する事象を計算するものです。It calculates composition of velocity with the aspect called the conversion of the speed.
We can calculate the difference of the elapsed time using proper time.
In other words I calculate a phenomenon to progress simultaneously.
点Kから2方向へ飛行する宇宙船の時間関係
Time for spaceship relations flying from point K to 2 directions
速度uの固有時間がv1の固有時間と同じとなる理由
The reason why proper time of speed u becomes same as proper time of v1
固有時間の関係が確定した。
次、宇宙船が帰ってくるということは
Relations of the proper time were settled.
Next, a spaceship coming back
宇宙船Bの経過時間がたとえどんなに多くても(船員はより多く年をとる)、それが帰ってくると経過時間は宇宙船Aより少なくなります。
(注意)加速度と減速度の影響は無視されています。
Even if there are very many elapsed times of spaceship B (the sailor gets more old), the elapsed time decreases from spaceship A when it comes back.
(attention) acceleration and the influence of the negative acceleration are ignored.
経過時間が小さくなる理由。
追いかける宇宙船の速度は逃げる宇宙船の速度を上回らなければならないから。
The reason why an elapsed time becomes small.
Because the speed of a spaceship running after it must exceed the speed of a flying spaceship.
速度計算の図
Figure of the speed calculation
力学の観点から見て
from a point of view of the Mechanics
計算例 Calculation example
ここで気がついたんだけど、宇宙船が帰ってくる計算はこれと同じでないといけないはず。
I noticed here, the calculation that a spaceship comes back should be the same as this.
それで、時計の使い分けをイラストしてみました。
ストップウォッチで示した時計は多分に力学の観点から方程式を解くのに使うという意味でイメージです。
Thus I performed an illustration of the use of the clock.
A lot of clocks which I showed with a stopwatch are images in the meaning that I use to solve an equation from the viewpoint of dynamics.
なので、L空間のK空間への射影が必要。
固有時間τv1を計算する。
I derive proper time τv1.
1. L空間全体は垂直方向の速度v0のみ持っている。 その固有時間τv0である。L空間全体は水平方向には速度を持っていない。
2.τv0での水平方向への物体の移動速度は V1X = v1x / τv0 となる。
これの固有時間をτV1Xとする。
3.水平方向への物体の移動速度 V1Xの固有時間を計算する。
4.前項で得られた固有時間をτv0を乗じることによりK空間の値に換算する。
1. The whole L space has only vertical speed v0. It is the peculiar time τv0. The whole L space does not have speed horizontally.
2. So the movement speed of the object to a horizontal direction in τv0 becomes V1X = v1x /τv0.
I assume the ropertime of this τV1X.
3. I calculate proper time of movement speed V1X of the object to a horizontal direction.
4. I convert peculiar time provided in a foregoing paragraph into a value of the K space by multiplying τv0 by it.
さて、定点Lを置く地点を決める方法を知ることができました。
By the way, I was able to know the method to decide a spot to put fixed point L.
This is an example
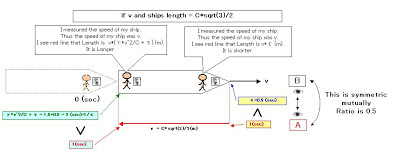
一般的に知られている以下の関係を考察する。
これは局所的に相互に対称的である。
これは大局的には非対称である。
Generally, I consider the known following relations.
This is symmetric mutually locally.
In perspective this is asymmetry.
これで終わりにする。 図を描くのは大変だ。
もう書ききれない。
I make the end in this. It is hard to draw a figure.
I cannot write it anymore.