積分の複素数近似 その9 :Complex number approximation of the integral calculus No.9

前回の記事で運動する物体を距離０でエネルギーを計算する場合は時間がγ倍に進んでいるのではないか？ということでした。

この距離０という意味は「相対的に距離０」という意味です。
つまり遠く離れた事象であってもその地点の観測者（Bとします）と相対速度が０（私、観測者Aに対して）であればその地点では運動する物体のエネルギーは時間の進みでγ倍になっているということです。

このことについて光のドップラー効果との関係を調べてみました。

ところでもはやタイトルとは直接関係ない感じになってしまいましたが、まあ趣味でやっていることなのでたとえばかばかしいテーマであってもなにか動機がないと勉強する気にならないものですね。  逆に言えば私のレベルではどんなものでも（たとえばかばかしいと思えるものであっても）テーマを持つのが重要な気がします。 まあ犬も歩けば棒に当たるということでしょうか。

ドップラー効果も特殊相対性理論と関係すると本当に興味深いですね。

下図は前回航路図から計算した光の到達時間と距離の図です。

------

これを観ると時間(Y軸 Ct)と距離(X軸)の値がドップラーになっているようです。
時間と距離は必然的に対称になります。

このままでは検討しにくいのでもっとわかりやすい図にしてみました。
この図では宇宙船が観測者に対して運動しているのではなく観測者が宇宙船に対して相対運動しているとしています。  この方がよくわかるようです。

ドップラー効果を計算するには歯数の消化率で計算しています。
宇宙船の長さL（船首から観測の基準点まで）は基準となるように L = Cとします。

なので宇宙船の中では光は1秒で船首から観測の基準点までの距離 L=Cを走ることになります。

------

船尾側から観ると向かってくる光に対して遠ざかろうとしています。
この場合は時間軸Yの値を用いると良いようです。

なぜ時間なのか？
それは船尾から出た光が観測（つまり検出器に衝突）できる地点での値だからでしょう。

この船尾からでた光は船首で発光した光がスルーして出てくるものとします。

一方船首側から見ると（観測者Bが）向かってくる宇宙船に対して観測できるのが自身の位置を起点とした宇宙船の速度と船長です。

と、書いていて、図を観て、すると本当にそうなのかこんがらがって来ます。
まったく対称性は地獄か天国か？
立場をひっくり返しても同様に成立するので本当にこんがらがってくる。
こんなものはまともに相手してはいけない。 じゃあどうするか。 結局幸いにもどちらも成立するので慣れしかないじゃないでしょうか？

で、時間で見るとドップラー効果に対してははその逆数が働くようです。

船中では長さがCなので時間は１sec、それを外から観測するとどうなるか？
例えば外から 0.5 secで観測したものは船中では1secであるはずです。
つまり船中で F hz の光はドップラー効果を含めて外からは *1/0.5倍、つまり2倍であるはずです。

一方船長を見る場合（船首側での観測者Bが）は船中ではF hzの歯数を消費しているが外から見るとドップラー効果を含めて 0.5Lとなったものは外からは歯数は 1/2倍になるはずです。

結局ドップラー効果は船尾側では時間の逆数倍になり、船首側では単位長 Cの何倍になるかということになります。

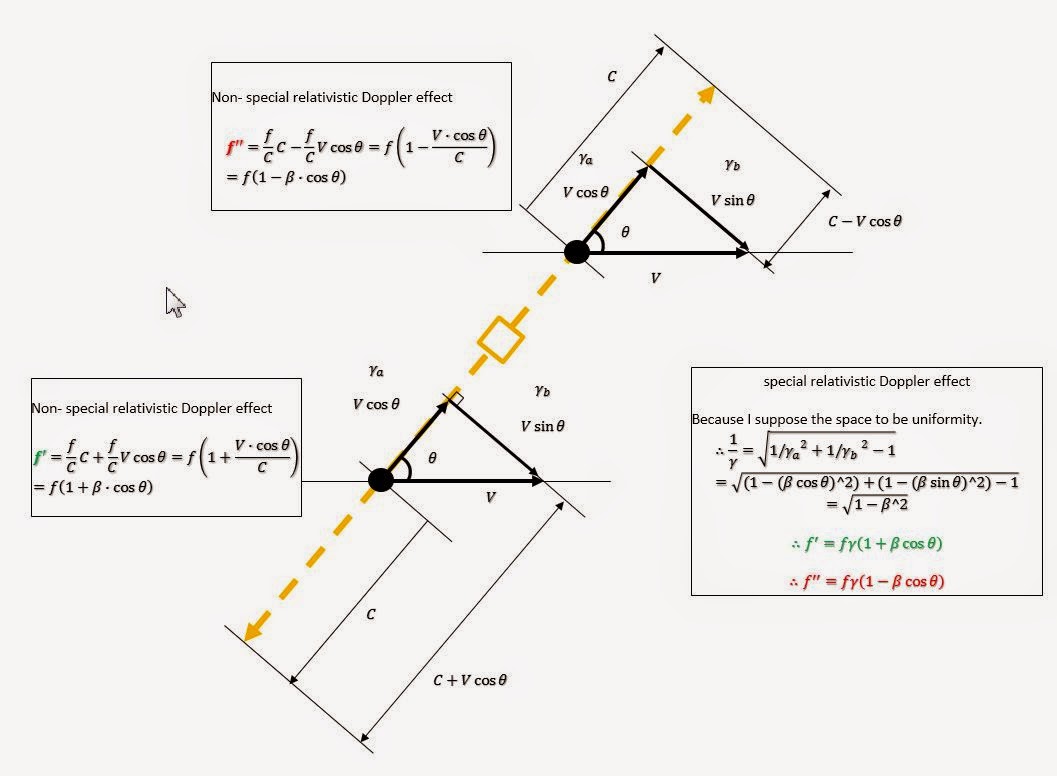
ちなみに角度θで観測する場合は下図のようになるようです。
位置関係で上と逆関係なっていますので注意。（左が船首、右は船尾側の対応です）

ところが、いろいろ調べてみると角度θでのドップラー効果は次のようになります。
これのθ = π/2 の値は実験で確認されているとのことです。

なので上のどこかがおかしいということになります。

思い当たるのは光に向かってドップラー効果の計算で非相対論に合わせて形式を変更したところです。 つまり本来は図の関係で得られた式を素直に使えば良いのですが非相対論の形式に合わせこんだ部分ではないか。 式の変形ができたのはたまたま θ= 0 の場合だけだったのではないのだろうかということです。

ということで無理に細工せず図から得られた式をそのまま使うことにしました。
下に変更部分を示します。

また角度を持った場合の使い分けですが対称性とか考えると次のようではないかと思います。

どうも煮え切らない感じになってしまいました。 私のレベルでは断定したくてもどだい無理です。
ということで勉強中の資料という感じになってしまいました。

ところで光の場合、船尾と船首側でγの使い方が異なるかもしれないなどということになってしまいましたが船尾側の時間γ倍はどうなるのかというとこれはγ倍で良いだろうという気がします。

ここで前回の課題であった最大の問題は宇宙船の中の時間が船尾側でγ倍進んでしまっているということであたかも未来が観えているのではないかということです。

いろいろ考えましたがこれは因果を考えれば船首側での事象は 1/γです。因果の因が1/γに因果の果であるγをかければ γ/γ=1 で １を超えることは無いということで問題ないのでは？と推測しています。

あと、例えば物の運動エネルギーがγmC^2 というようにγ倍になる、これは宇宙船の船首側では 1/γでは無いのかということです。

物質と光とは異なるとは思いますがγが時間の進み遅れに関するものであるからなにか共通の影響があるとも思えます。

これは宇宙船の外にいる我々が速度V、距離0 で観測した場合でしたが結局わからないです。
光の場合は特殊だとも思えますが・・・。 なのでこれは今後の課題にしよう。 というか、もうそんな時間は取れないかもしれませんが。

後、気になるのは関連してきになるのは人工衛星の時間の関係です。
人工衛星は距離が一定で周回している場合時間が進むそうです。 それに周回速度による時間遅れが加わえて計算できるそうです。 これは一般相対性理論で計算できるそうですがこの時間の進みとなにか関係があるのかもしれないとすれば興味深いですね。

-------------
2015.3.2

いろいろ見直中ですが、角度によるドップラー効果は次のようです。

cosθが分母にあるかまたは分子にあるかは大きな問題です。

θが0とπではドップラー効果に関係があると思われる(1-β）は入れ替えるように変形できますがそれ以外では角度を持つと一筋縄ではいかないと思われます。
なぜなら、例えばθが π/2の場合速度があると実際に観測器に届く光は後方で発光した光だろうからです。 その結果 1/γ に見えているだけなのかもしれません。

特殊相対性理論による周波数の変換がγ倍であればと期待していましたがなかなか難しいようです。

例えば光は船尾をスルーして出てくるとしていますがこれを船尾に光の中継器を置いたとして、この中継器は間髪入れずつまり時間遅れなしに入力周波数と同じ光を放出できるとした場合これは発信器と考えても良いわけです。

この発信器が元周波数 f を発信するとする。 これが相対性理論によりγ倍になったら光の場合はその周波数で距離が生じても走り続けるはずです。 つまり距離 0（0でなくても距離が一定であっても） で速度Vの場合の作用はγ倍であると言えるのでは？と期待していたのですが。

 まだ何かあるのではと期待してはいるのですが、  f ' = fγ(1 + or - β) の形式の方がドップラー効果として自然に思えるということだけでは残念ながら結局なんともいえないのと同じですね。

とにかく、θが0とπ 以外の場合を分析するには私のレベルでは無理っぽいですね。 なにかほかの方法を考えた方が良いかもしれません。

-------------
2015.3.3

どうにも行き詰まってしまったので何が原因なのかを調べてみました。

どうやら結果の式から色々調べようとして変形できないかを試していたのですがこの式はこれ以上変形できません。 cosθが(1-βcosθ)だけに入っているのが原因です。

θが0とπの場合はcosθが1,-1となるのである種の対称性が復活して変形できるようです。

つまり、これ以上メカニズムを分析しようにも結果を弄繰り回しても無駄だということです。
この式は計算結果がわかるだけです。

ということはこの式は何らかの操作の結果であろうということです。
その方法を見つければ光の周波数が相対性理論によってどう変換されるかわかるかもしれません。

で、式を見ていて、たぶんこれではないかな？と思うものを見つけました。

特殊相対性理論でのドップラー効果は光の向かう場合と光から遠ざかる場合で下の式形になるだろうと仮定しています。

光に向かう場合は船尾側から船首までの光を船首側から観測する場合です。
光に向かうのでドップラー効果により圧縮されて周波数が高くなります。

光から遠ざかる場合は船首から船尾側に飛ぶ光をポイント0地点で観測する場合です。
つまり、速度Vの粒子を距離0で観測することに相当するものを光の周波数の変換の様で推測しようという意図があります。

下図はその式形です。 式を変形することで通常のドップラー効果の式に類似のものが得られています。

で、その方法ですが、わかってしまえばああこんなものかと納得がいくのですが、速度Vとその光の方向分(Vcosθ)の固有時間の逆比のようです。

それが次の図です。

Vの光との直交分(Vsinθ)は上の点線で示した方向で縦のドップラー効果ですが、これがγc/γを乗ずる理由だと思います。


で、結局周波数はどうなるかですが、θが0とπの場合はドップラー効果のかかり方を見るにγ(>1)倍されると考えて良いと思います。 静止時の周波数fのγ倍です。

ところが角度を持った場合は f(1/γ)(1/(1+,-βcosθ))のように1/γがかかりあたかも低くなるように見えます。 だけどこれは (1/(1+,-βcosθ)) の項で逆に補正されています。

従って、本来はγ倍されるとするのが自然だと思います。

そう考えると速度Vの粒子も(距離0 または一定で)光も同じくγ倍でエネルギーが高くなると言えるのではないでしょうか？


-------------
2015.3.5

Vのsinθ方向には光が無いので当たり前ですがドップラー効果は生じません。
光に平行な方向には生じます。
これは、Vに沿った方向に検出器が運動しているとしてもまた仮に光が来ているとしても同じです。
ドップラー効果はcosθ方向のみに生じるようです。

ということは、上の記事のγcの変換は純粋に固有時間だけの変換です。

この変換は以前下記の記事中でやったので再掲しておきます。

最後の式はわざと ^2 しているのでルートがとれているだけです。
とにかく、この問題はちゃんと数式で決着がつくものです。

三つ子のパラドックス3 triplets' paradox 3
http://akimpotos.blogspot.jp/2013/02/2-triplets-paradox-3.html

このときは闇雲に計算していただけだったが、ドップラー効果を勉強することでこんな区別があることがわかるとは驚いた。 というより相対性理論がドップラー効果込みとは・・・。 考えてみれば当たり前かもしれませんが。

後は、θがπ/2 と 3π/2 のとき f' = f/γ となる理由です。

θが 0 と π時には fがγ倍されるのにこの場合はどうして 1/γ となるのか。
周波数が小さくなっています。  言葉で言うのは難しいので図でしますが、この図表現方法が結構難しい。 おまけに相対性の対称的な性質からどうにもこうにもこんがらがってしまいます。
だけどもたぶん考えからは間違っていないと思います。 ほかにもっと良い表現方法があるかもしれません。

で、宇宙船を１辺 L=C の正方形として正規化します。

光は上下に走るとして、光路図を流用して表現します。

結局光は宇宙船の上から下まで縦 C(m) を1 秒 で走るとすると、静止系からはγ秒かかることになる。 宇宙船の中では光はfの歯数を消費する。 これが静止系からはγ秒(1秒<)となるので同じ歯数なら周波数は低くなる。 従って f' = f/γ となる。

考え方は間違っていないと思いますが、とにかく表現が難しい。
とにかく、切りの無い話になりそうなのでいい加減この程度にとどめておきたいと思います。




-------------
2015.3.7

この際なので光の経路について図にしておくことにしました。

線9,12は下の箱に書いてもいい。 上下の線1,10,7,6 は経路をイメージするのに少し工夫する必要がある。

しかしこれはおかしいようだ、縦と横しか合ってない気がします。


-------------
2015.3.12

宇宙船の箱を割り当てることにより斜めの軌跡も表せるかもと思ったんですがどうも無理なようです。 考えてみれば変換が時間を含めてt,x,yの3次元になるので原理的に駄目だと思います。

では、なぜ縦と横の場合は何となく表すことが出来ているようだ？ ということはどういう意味だ。
たぶん、横の場合（x,ct軸）はy=0、次に縦の場合（y,ct）はx=0ですがこれは xでもyでも対応関係は一緒なので多分xに対応することもできるのでは無いかと思います。 つまりお互い直交している部う分で共通する部分があるということだと思います。 どちらにしてもこれ以上はあまり意味が無いので止めることにしよう。

積分の複素数近似 その8 :Complex number approximation of the integral calculus No.8

前回は運動する物体の物質波の周波数を下のようではないのかと推測していました。

しかし相対性理論によると運動する物体の時間は静止時の 1/γ となります。

つまり回転数は下がることになります。

なのでなにかおかしいのではないのかとゆうことになります。

ということで最近続きを考える余裕ができたのでまとめてみることにしました。
とはいっても人生いろいろありまして余裕といっても後2ヶ月ほどですが。
おまけにPCも買い換えまして、お絵描きに使っていたエクセルも2013にバージョンアップしました。
速度は体感的に20倍程も違うでしょうか？
しかしリボンですか、なれると結構いいんですがメニュー式になれていたのでほんときついですね。


さて、とは言ってもこの結論、あるにはあるのですが、なんといいますか我ながらあまりにばかばかしいことになってしまいました。 まあメモ代わりに残しておこうと思っています。
まあ素人の間違いとして結構おもしろいかもしれません。

それで特殊相対性理論で以前やった光航図のおさらいということです。
あの投稿は図を描くのに一生懸命で計算まで載せる余裕がなかったのですが、私自身も忘れそうになってましてどこかに残しておかないといけないということで一から記入していきます。

まずは時間と空間の変換をおなじみの座標で表していきます。
この図は座標変換の規定の関係です。
変換後の基底の読み値を１とした場合の変換前の基底の読み値との対応です。
左から右へ青い丸の読み値が順次γ倍になっています。
変換式が対称行列なので値も対称なものとなります。
なので距離化時間軸も同じ値となります。

これに黄色で示した光路を加えて幾何を計算します。

これにおなじみの宇宙船のイメージを加えます。

赤が宇宙船の内部の時間関係です。 この図は宇宙船の内部が単位１です。しかし外から見るとその時間関係は回転しています。
外からは運動する宇宙船は1/γ倍に縮んで見えています。 時間軸も対称なので同じ関係です。

で、今回調べたいのは時間軸だけなのでそこを変換を強くかけて判りやすくしました。
ですのでこれはイメージ図です。

この図でγ倍となるところを探していくと爆発マークの所が怪しそうです。

この図では、計測を開始した ｘ＝０ の地点で時間が1/γ、たとえば0.8秒経った時点で宇宙船の在る基底の時間は １秒でγ倍となっています。

なのでもし宇宙船の中で回転数を計測できたとしたら例えば回転数は毎秒1000回転としますと、外からは0.8秒で1000回転なので外の世界からは見かけでγ*1000=1250回転となります。


したがって運動する物体の物質波は静止時のγ倍ということになります。
とはいえ、このままでは何がなにやら分からない。何の対応なんだということになります。

なので次のように考えるのはどうでしょう？
計測の基点は宇宙船の船尾でなくてはならないということではないのでは？
例えば宇宙船の中央の星印を起点とします。  分かりやすくするために宇宙船に窓を追加しています。

すると面白いことになりました。
座標変換の式からは当然なのですが ｘ＝０ 地点である時間に宇宙船の対応する点を観測するとすべて宇宙船中の１秒の時点が観測されることになります。 ！！

とはいえ実際にわれわれが見る宇宙船は青い図で示すように Ｘ＝０地点からは対応する所を観測できません。 どんなに近くを宇宙船が通っていたとしても実際に観測できるのは直近の部分だけでしょう。 たとえ宇宙船が遠くに離れていたとしてもそれはそれで空間が離れているのでどうなるかは私にはよく分かりません。

この図を観ると、時間の遅れは実際には距離を生じていないと発生しないのではと改めて思わされます。 よくよく考えてみると変換式の機能から当然ですが。

だから距離が発生しない場合はどうなるのか？ ということが問題です。
イメージ図にすると次のようになります。
宇宙船は仮想的にごく近くを飛行しているとします。
ええと、なんですか、つましまああれです、ここから次々を窓を観ていくと、常に経過時間のγ倍の宇宙船が観れるという事です。

「宇宙船の窓に未来がみえるよ!!」   「やったね たえちゃん」

・・・て、酷い・・・。 これではオカルトです。 どこでどう間違えているのか私にはさっぱり分かりません。

ひょっとしたら相対性理論のことであるから起こりうるのか知らんとも思ったりしますが・・・。
また相対的に観ると相手側からはこちらの未来が見えていることにもなります。
まあ、相対論というものはそれでも物理的に問題ないよと主張しているものですからいいのかもしれませんが・・・・。

それにこんな関係は例えば粒子を加速して標的に当てるのをごく近くで観測した場合にもいえることです。 その粒子は未来時間を飛行していたということになります。

ということで実に悲惨な結果になってしまいましたが、素人の私からすればそういうところが返って面白いものです。しかし、 こうなると前に投稿した光の航路図も怪しくなってきました。 まあ本気にする人はいないと思いますが念のためご注意。   文字通り御笑覧いただければ幸いです。


--------------------
2014/12/12

冷静になって考えてみたら次のようなことではないのだろうか？

1) 特殊相対性理論は単に経過時間の尺度を計算しているだけなのでは？

2) そうであれば x=0 地点の経過時間尺度と x=0 地点から宇宙船の星印を観測している場合の時間尺度が違っても問題ないのでは？ 宇宙船の星印は距離が生じているので時間尺度が 1/γ になる。 つまり宇宙船の中は時間がゆっくり進む。

3) x=0 地点では宇宙船の中はγ倍時間が早く経過する。 これは未来に進むというよりもx=0地点に近づくまでは距離が生じているのだから遅れている（？）はずだ。 これが x=0 地点ではγ倍になり後離れて距離を生じると遅れになるのでは？ つまりγ倍の進みは x=0 地点だけの特殊なものなのでは？

4) もしそうであれば窓から未来が見えるなどというオカルト的なことにはならないのでは？

5) このようにいろいろ見かけの値が変わっても物理的な計算には相対性原理により支障がないというのが相対性理論の思想では？

6) 例えば粒子の弾性衝突等に使用する値はもちろん x=0 の値を用いるのが自然であろうと思う。特に波動に換算する場合はそうでないとエネルギーのつじつまが合わないだろうし。


とにかく、私としては未来が見えるなどというばかげたことは絶対起こるはずが無いと思いますね。


--------------------
2015/1/1

• エネルギー対応について

特殊相対性理論での下記のエネルギー対応、確かに対応関係は計算してみれば分かるが物理対応がいまひとつピンとこなかった。

これはひょっとして下記のような回転に関する対応関係ではないだろうか？

何か対応関係として不思議にしっくりくるような気がする。

ただし 2*pi*k*f は光速Cではないので注意。

ところで今までの記事の立体球の回転は駄目そうな気がする。 緯度による分力の計算が入ってないので0にはならないが少し小さくなるようだ。 複素数計算だけあって２次元で完結しそうな気もする。

なのでもし回転体であれば円盤か輪であるような気がする。  まあ今となれば書きっぱなしで本気で見直す気も無い、というより気力がないだけなのだけど。

後、回転半径を計算するのに結局留数のエネルギー値は使わなかった。 これは γmC^2 = hf で出した回転数を優先して使用したためだけど、 なかなかうまくはいかないね。 だけど留数計算がエネルギー関係の逆演算かもしれないというのは結構面白い。 

----------------
2015/1/18


エネルギー対応でエネルギーをベクトルのように計算している理由は次のとおりだと思う。

1.    質量エネルギー mC^2 と全エネルギー γmC^2 は同じ物理対象物が運動するかしないかの違いだけなので物理的には同じ一つの物だろう。

2.  つまり運動エネルギーは質量エネルギーが運動することにより変化しただけであるとも考えられるのでは？ 運動することにより時間が進み、ということは観測者のほうが時間が遅くなる。
ところで、相対性理論の γmC^2は時間対応が逆の場合なのでは？


3.  この関係図は

• エネルギーはスカラなので進行方向のエネルギーYは差分
• 運動量はベクトルなので三角の関係
• 進行方向の運動量はエネルギーがわかっているのでこれから速度Vに対する運動量が計算できるので既知

ということで実質一つの物理的実体のエネルギー mC^2 との関係なので mC^2 = KPx と一次の関係で表せれるとすればエネルギーをベクトルとしても扱える。 つまり運動量を扱っているのと同じだろう。 もちろんKは現時点ではどんな値（または式）であろうともかまわない。

えー、なんと言ったらいいのだろうか？ とにかく今扱っている回転体とはそんな関係が成立するような物なのでは・・という意味です。

つまり質量エネルギーも何らかの回転体のエネルギーであるならばこの関係が成立するのでは？

一方、進行方向の速度Vの運動量は以前の記事にあるようにエネルギーから計算できるとすれば

これは既知の項目。

ということで係数 K = C ということがわかる。 

なので、質量エネルギー mC^2 に対応する 運動量が得られる。

結局、エネルギー対応から質量エネルギーの運動量が得られるということのほうが重要なのでは？

思うところ、質量エネルギーも何らかの回転に関係するエネルギーであるとすれば、エネルギーをベクトルとして扱うと運動量の関係になるというのは面白いねえ。

ということは相対性理論も何かしら回転と深いかかわりがあるでしょうね。

ところで、すべての物質が共通して持つ物と言えば 「空間」であるから量子力学の初歩で聞かされる不思議な話の数々の犯人はすべて空間におっかぶせることはできないのでしょうか？

とにかく不思議すぎて犯人もわからず捜査している探偵のような気分になりますよねえ。
まあ世の中その方が面白いのかもしれません。

積分の複素数近似 その6 :Complex number approximation of the integral calculus No.6

--------------------
2014/5/11

続き

http://akimpotos.blogspot.jp/2014/04/5-complex-number-approximation-of.html


--------------------
2014/5/13

回転エネルギーを体積から計算する前にぜひとも解決しておくべき問題をまず片付けておく。

前回の続きで体積からの計算をしようと思ったのですが、それは多分まず間違いなくできると思う。

それよりも解決すべき問題とは、力が円周に継続してかかり続けるものだろか？ということです。

とにかく、今はそれぞれのパーツを確認している段階ですが、重要度の高い問題をまず解決しておきたい。

上の式を見て回転エネルギーを計算するのに力が継続して働いているという計算式になっている。

力が継続して加わるということは継続して加速度運動をしていることを意味している。
実際こんなことがあるのだろうか？

そこでまず回転に伴う向心力について観てみる。

向心力は次のようにして計算できる。

m は円周を一定の速度 v で回転している。

向心力 Fa は mv^2 / r となる。

ここで、注目する事は

1. 分母が半径 ｋである。 つまり 1/k である。 これは中心のエネルギー Ek が2次元では同じく 1/k になることである。 
2. 分子は mv^2 である。 これは運動エネルギー  mv^2/2 と何か関係がありそうである。

今までの記事を書いてきて、これは何かあるはずという直感がある。

このテーマがなければ、留数計算と向心力に何の関係があるのかと思うだろう。

しかし、今、私は 留数計算の背景にはある物理モデルが存在するだろうという思いが強い。

上の向心力は速度ベクトルの関係から求めたものである。

しかし、微小膨張収縮モデル、つまり仮想分裂モデルでは実際の飛行経路が必要である。

上がその経路である。 みかんの一房が反時計回りに回転するときにΔθの一刻みの経路である。

微小経路は近似式である。 赤い線で示す向心力の経路は kΔθ の更に Δθ を乗じたものになる。

幾何的経路で計算した経路長 dl'  と向心力 Fa による計算から得られた経路長 dl は同じになる。

したがって幾何的モデルは上で正しいと思う。

lim Δθ-> 0 で向心力のベクトル（赤い矢印）は限りなく正確に中心を指すようになる。

また、青いベクトルで示す回転ベクトルも限りなく正確に接線方向になる。

問題は向心力から回転のエネルギーを得る方法である。

此処までくると推測するのは難しくない。

Δθの一刻みで定速度 v まで加速してやれば良い。そうすればΔθの周積分で計算できる形にすれば 1/2π でキャンセルするだけで回転エネルギーが得られるだろう。

その式では加速度が円周に継続してかかり続けるように見えるのだろう。

此処で気づいたのだが いままで複素数 1/z で回転エネルギーを計算するのに留数計算の2πのキャンセルはいらないだろうと思っていた。

しかし、上のようなものであればこれは必ず必要な意味のあるものではないか。

つまり留数そのものが中心のエネルギーではないのかということである。

上の図で明らかにわかる矛盾は赤い向心力の経路と青い円周方向の経路の終点が一致しないことである。

とりあえず円周方向で 速度 v まで加速させてみよう。

上で求めた円周方向の加速度 B は B = 2v となり矛盾が発生している。

また向心力の経路と円周方向の経路の終着点が一致しない。

これはどういうことであるか？

回転エネルギーも求めてみる。

向心力を求めた式では幾何的な経路長と、加速度により求めた経路長は一致している。

なので向心力については問題ないだろう。

この矛盾は何処から来るのだろうか？

式の表すことを素直に解釈すれば

• 円周方向の経路は長すぎる。 だからエネルギーが2倍になる。

これと終着点が一致しないことを考えると、エネルギーを正しく導くためには次の関係でなければならない。

これであればエネルギーも正しく計算できる。

しかし、下の拡大図あるように円周方向の経路長が弦を越えて下に入っている。

これでは半径方向に無視できない程の経路がありエネルギー差が円周方向のエネルギーにもか

かわらずポテンシャル差が存在する。

これは明らかにおかしい。

だけど、これは微小部分を目に見えるほど大きく描いているのでおかしいと感じるだけのようです。

究極では青い線も、ピンクの弦も、黒い接線もすべて接線に限りなく近づく。

一見するとイメージに騙されそうになります。

だとすれば、これは一体どういうことかと一日悩んだあげく気がついた。

式が示すことを信じるなら上の関係になるはずです。

Δθ --> 0 で全体として接線に限りなく近づく。

近づき方も素直な感じでありエネルギーが何らかの比例関係で制限される様子も無い。

究極的には円周上を這うエネルギーが得られると思う。

私としてはピンク線の弦の上に綺麗に乗っているような図を漠然と想像していました。

なのである意味、崩れたような上の図は少し驚きました。

しかしよく考えるとこれでも理があります。 究極的には円周に沿えば良いのですから。

点線で示される経路が膨張です。 実践で示される経路が収縮です。

同様に力では向心力と遠心力になります。

仮想分裂法では反発と押込みに対応する事になります。


--------------------
2014/5/30


時間の取扱いが明確でなかった。

微小膨張収縮では慣性エネルギーを計算するのに進角のΔθの１刻み毎に 速度 0 から慣性速度 vまで加速させているわけです。

だから計算に使う時間も単なる時間ではないと思う。

区分けのために Δθの１刻みの計算に使う時間を内部時間 t'、その計算に外部から与える時間（積分範囲の時間） tを外部時間と呼びます。

この時間スケールの違いは向心力の方向と円周方向で同じにならないとおかしいわけです。

計算するとその関係は両者とも t' = 2t  という関係です。

どうやら内部時間は外部時間の2倍早くないとちゃんと計算できないようです。

これで、 半角 Δθ/2 、時間 Δt / 2 の間に得る速度を計算すると 慣性速度 v と計算できます。

ということは詳しくは計算などできる段階ではないのですが 1/z の積分には半角の関係もあるということでしょうか？

後、気になることは微小膨張収縮法では3次元の場合球全体が圧縮膨張するわけですが今までの計算を見てわかるようにj軸に並行する分は計算に入っていません。
もっとも電気的な作用では軸に平行な方向分は回転による面積を生じないので計算しないでも良いのかもしれません。
機械的ななぞらえのものであっても同様で軸に並行分はやはり作用しにくい。
だけど横から見るとそれにも軸方向の面積が生じることになります。
だけどこのような回転がどのようなものなのかは私には想像もつきません。
なのでこのテーマではあくまでもある軸を想定するとその回転だけについて限定しようと思います。


--------------------
2014/6/5

試みにもし電子が半径を持つとしたらどうなるか計算してみました。

電子の半径の計算は調べてみると色々な考えもあるようだけど現在のところどれも定まってないよう
です。  電子に半径は無く点であるという話も在ります。

しかし、もし半径があるとすれば

http://ja.wikipedia.org/wiki/%E9%9B%BB%E5%AD%90

にあるように   理論値 1.0×10⁻³² m   =<  radius < 実験値  1.0×10⁻²² m のようです。
このテーマの場合は エネルギーが定まれば E = hf / 2  の関係で回転数 ｆ が定まるとして計算してみます。
この回転数を得るためには 半径 k がいくらでなければならないかが決まるのでは？ ということです。

というのはもし回転しているとすれば、回転するためには 1/k に対応する向心力が無ければ回転しないんですから。
つまり 半径 k が定まるということです。

向心力としては引力であろうとクーロン力に対するものであろうと同じ働きを持つようですので応用できると思います。

上の式を計算したものが次になります。

半径 k = 2.444   10^-26 となり理論値 10^-32 よりはかなり大きな値となってしまいました。

電子に適用するとしても半径の問題は難しすぎるのでこれ以上は進展はなさそうです。

だからこのテーマは 電子云々については諦めて（当に諦めてはいましたが・・・）、単に 「留数の物理イメージを探る」 という範囲に限定したほうがよさそうです。

それでも今まで謎だった 2πのキャンセルの必要性だとかが具体的に解ったし、素人のテーマとしてはそのほうが結構意義があるようです。 まあ教育用のトリビアねたにはなるかもしれません。

私自身としてはいままでの記事でほぼパーツを集めれたと思うので最後はこれを纏めたいと思うのですが、なんかパーツを集めただけで満足してしまって纏めるエネルギーがなかなか湧かないのが悩みですね。



--------------------
2014/6/8

上の計算の補足事項

1.   Ek と 運動エネルギーは非常に小さいようだ。 なのでこれで半径を計算すると非常に大きい。 従ってこれが半径を決めているとは考えにくい。

2.   では何が半径を決定しているかということになるが、質量エネルギーが原因であろうと仮定した。 質量エネルギーで回転数が決まれば半径が計算できることになる。

3.    向心力はつりあっている反発力と等しいだろう。  電子を鋼体的と考えると反発力と等しい向心力を持つと仮定した。

4.    ポテンシャルエネルギーは対数 ln (k) になるが、これと半径の関係も考えられるが、対数なので半径が非常に大きくなるので要因とは考えにくい。 また、これは微小膨張、収縮に伴うものだから本来相殺されて 0 になるべきものとして計算に入れてない。

5.    Ek は半径 k によらず一定の値になる。 回転数が質量エネルギー Em で決まるとすれば Ek は Em に添う（イメージとしては例えば伸縮性のある服のように Em という体に自然にフィットして）ことでそれの向心力を計測するセンサーのような機能をもつエネルギーであるとした。 とすればEk の向心力で半径 kを計算できる事になると仮定した。


後、このテーマでぜひ明記しておきたいこと。

1.    電子自身の計算では、もし電子というものがこのテーマで論じた構造に準じた構造を持つ場合（概念的なものを含めて）、複素数 1/z の項は3次元での力 1/z^2 を積分する前に2次元に縮退したものではないのか？ つまりこのテーマでは向心力になる。

2.    実数近似とした場合、 力は z = k + id -> k  （if k  >> d)  となりあたかも 力 1/k^2 を積分したものと同じになる。

3.    複素数の世界では 直線部のエネルギーは 対数 ln() になる。 しかも実数で出る。

4.    なので、電子には力とエネルギーに意味の重複を起こさせる何かの隠された構造があるのではないだろうか？  もし点ではなく何らかの構造があるならば、うーん、何でしょうか？

5.    もしそうならば、 1/k は力なのでエネルギーの計算に入れる必要は無い。  ln () はエネルギーだがこれは微小膨張、収縮に伴うものだから本来相殺されて 0 になるべきものでは無いのか？


--------------------
2014/6/15

めも

1.     1/z は円周に対応する。 イメージとしては正確には円周上を回転する点電荷 q を表す。

2.     1/z^2 は球の表面に対応する。  イメージとしては回転する球の表面を表す。内部がつまった物ではない。 今までの計算では内部が詰まったものとしていたがこれはガウスの法則に合わない。 なぜなら中心に近い殻の部分は中心の仮想電荷が変化するはずであるから。  幸い計算結果に変化はないはず。 なぜなら電荷 q を表面に均等に分布しているとすれば良いだけだから。

3.    なので3次元世界では 電荷は球の表面に均等に分布していると思う。

4.   1/z^3 は内部が詰まったモデルをあらわすと思う。  距離の３乗になる理由は 2. 項のガウスの法則による中心の仮想電荷が変化する為だと思う。  多分ちゃんと計算すると辻褄が合うと思う。
だけど、これは4次元球の表面（４次元球の表面なので3次元になる）なので3次元世界には存在しないのではないか？


--------------------
2014/9/9

2ch の物理板を見ていたら 「量子チェシャ猫」の話題があった。

どうも粒子と空間は非常に密接な関係にあるらしい。 ほとんど一体として扱うべきなのかもしれない。
そう考えるとこれも意外とありえるのかもしれない。
エネルギーが空間のゆがみで自然に回転するとそれが粒子になるのかも。
粒子が運動すると螺旋に軌道を描くと考えることもできる。 その軌道は予定航路のようなものであるとも考えられる。 軌道を完全に塞がない限りその予定軌道は分割されても干渉して位相の強弱で干渉するのではないだろうか？   と素人なりに想像してみると空間というものが空虚では無く、なにかしら物理的に何か物質に近いような物にも思えてきます。

あと、思い浮かんだことといえば、 複素数 1/z の積分、実数では 1/x の積分が log になる事だけど、log は回転のポテンシャル？と考えれば何となく納得できる気もする。
回転であれば今回転している状態が ポテンシャル0 ではないだろうか？
軌道が変わる場合エネルギー差がlogで計算する事になるのでは？

ところでこの世界では本当の直線運動って本当に存在するのだろうか？
短い距離では直線と計算できるだろうがマクロで観れば回転ではないのか？
そうなら 複素数で計算するのもあながち不自然では無いような気がする。

さらに、馬鹿なことだと思うのだけど、粒子が対生成して分裂した時もそれぞれは実際には楕円軌道である種の結合関係を保ちながら分裂しているのではないだろうか？
この場合は、中心にはある仮想電荷（ガウスの法則が働いているとして）なりがあって回転力があるのでは？   などと想像してみるのも面白い。

とにかく我々のいるこのいわゆる「空間」というものは実はとんでもない物なのかもしれない。
何しろ重力などでも歪むし、運動するだけでも縮むし、時間までもそれに合わせて変わるというのだからとにかくまともな物でない事は確かだろう。 更には粒子まで作り出すかもしれないのだから。