--------------------
2014/4/5
http://akimpotos.blogspot.jp/2014/03/4-complex-number-approximation-of.html
の続き
2014/4/6
複素数 1/z で表される仮想ポテンシャルによる力をみていきます。
仮想ポテンシャルというのは私が勝手につけた仮想分裂法によるエネルギーのバイアスのことです。
式の簡略化のため単位円とします。
dq がUターンする部分で蓄積されるエネルギーは仮想ポテンシャルによる力と円周長の積分で計算されます。
不思議なのは 1/z で計算されるエネルギーをさらに積分することです。
このことは一旦保留しておいて、とりあえず力のイメージを観て行きます。
力が 1/z^2 の形になることは次の計算事例から推測できます。
これによると力の方向は進角θ(theta)の2倍で回転していることが推測できます。
遊星ギアモデルに適用することもできます。
また、積分方向が円の接線方向であることから 1/z の積分は線積分のようです。
線積分であるということと、力の進角が2倍であることを考慮するとこれを組み合わせるのはグリーンの定理です。
これの微細部分は難しそうなので別途検討しよう。
エネルギーが面で分布しているのはどういうことか?
これは仮想分裂法であることから次のように dq は面内にある電荷を代表したものではないかと推測できます。
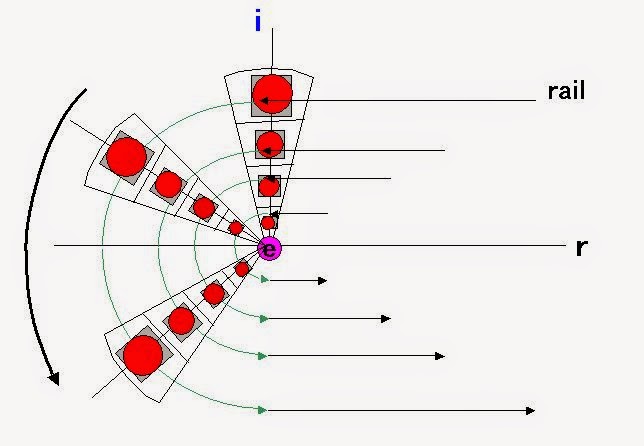
仮想法と割り切ると結構イメージの幅が広がるものですね。 仮想法、便利だ!
ところでこの面内の各点にある力の大きさは非常に大きな力になるのが気にかかります。
極に近くなればなるほど無限大に近づいていきます。
こんなに大きくて問題ないのでしょうか?
これは、案外問題ないと思います。
なぜなら、大きな力の近くで遊星歯車(イメージですが実際は点とします)を回転させようとすると同じく非常に大きな力をかけないとまわせないと思います。
要は回してもエネルギー収支が小さければよいと思います。
それで、際外周の力の様子を観てみます。
これは遊星ギアのイメージで示したものですが、実際は面名にある点ですから、これではなにかイメージがぼやけています。
で、これを実際に近づけてみます。
これを良く観てみるとここでも押込みと反発によりエネルギーの授受が行われているようです。
実際にはこの半円内は充実しています。
・・・という方針で今後検討してみようと思います。
多分、面積で考えるところが相当怪しいのでここで破綻しているような気がします。
まあ、面積で回転しながら通過するだけなのでこれでもいいのかも、今一イメージがぼやけてますね。微小な回転の集合と考えれば円周方向だけでなくその直交方向、つまり直径方向にも力と変異があるのでそれが計算されているとか・・・。
まあ色々とあって今後新しい勉強もできなさそうなのでだらだら妄想を楽しんでいこうという心境の今日この頃です。
ところで、電子が分裂したとするとすさまじい力で加速されるでしょうから物理モデルを詳細にしていけばすさまじいエネルギーが電磁波、光子(質量0でエネルギーのみ)として放出されるでしょう。
このエネルギーは仮想分裂法なので押込み側に入れ込んでやればよいのではないでしょうか?
そのエネルギーはlogで表されるようです。これは超関数によると log(r^2+b^2)/2の項にあるようです。
--------------------
2014/4/6
いままで 1/z はポテンシャルのようなものだと思っていましたが違うようです。
ポテンシャルは積分するような種類の量ではないので不思議に思っていたのですが。
円運動の部分に関してはこれはエネルギーです。
円運動する回転する微小部分のエネルギーの積分です。 つまり力と距離の積分です。
分裂した後の直線部分は虚数部分は小さいので無視できるとするとこれはポテンシャルとしても使えるという程度の性質のものです。
円運動するので微小部分はグリーンの定理で表される縦横の距離を移動することになります。
従ってグリーンの定理による面積分で計算できるということになるようです。
結局 1/z は直線部分と極の周りの回転部分ではその性質と意味が違うということのようです。
かつそれが連続した経路でも成立する。
これは、マジックのようでもありちょっとビックリだ。
いや、待て、もし仮に 1/zをポテンシャルと認めるとしましょう。
これを積分することで回転のエネルギーを出せるということは普遍的に成立するのでしょうか? 複素数化すること自体なにかポテンシャルとは別の意味になってしまうのでしょうか? 面白い課題かもしれません。 超関数を使えば直線でも計算できるのですから。 極の周りというのは面白い性質を持っているもんですね。
円運動する扇形の部分でエネルギーを計算したいのですが見るからに頭が痛くなりそうです。
ところで、仮想法が便利だなと思う点は、考え方が自由度が増すというのでしょうか割り切ることができます。 普通、仮に分裂すると粒子を構成する部分は上の図のようにU字にはならず半径方向に即飛び出していくはずです。 これでは経路が不連続になってエネルギーの計算はできないでしょう。 またキャンセルするための押込み側の経路はどうイメージすればいいのでしょうか?
これでは実際的と思われる物理的挙動にしばられてにっちもさっちもいけなくなります。
しかし、仮想法と割り切ってエネルギーが逃げないようすれば、つまり経路を制限することで計算できるようになるのではないでしょうか。 まあその為に無限のエネルギーが発生するんですが、それは仮想法の枠内でキャンセルすることができます。 逆に言えば無限の力とかエネルギーが発生しなければ計算できないともいえます。 なので無限の値というのは副作用というよりこの場合計算する為に必須であると言えると思います。
--------------------
2014/4/7
上の図では力の方向はマイナスを入れ忘れたので逆になるようですがイメージとしての辻褄ま合うので後で暇があったら訂正することにしよう。
1/zの積分がエネルギーだとすると仮想分裂法では面積で分裂しなければならない。
それは扇形の形でイメージできます。
この扇形が回転してグリーンの定理で表される面積部分をスイープすることでエネルギーが計算できると推測します。
扇形だと極に近くなると電荷が少なくなっていくので扇形全体では有限な値が得られそうです。
力と方向長が複素数でかつ各微小点の回転のようなので単純なことではなさそうですがとりあえず簡略化して計算してみます。
結果は i*4*dq となり有限な値となります。 1/z の複素数積分は これが i*pi*dq です。
約 i*3*dq です。
もし、力と方向長が複素数で回転エネルギーがこの複素数で計算されている性質のものだとすると 1/z の複素数積分はポテンシャルを積分したわけのわからないものではなく、やはりエネルギーではないかと思えます。
ところで、式を書いてるうちに電子の電荷とネイピアのeがごっちゃになってまいったですね。
--------------------
2014/4/11
1/z のポテンシャルでも計算します。
結果は 1/z^2 の力を積分したエネルギーと同じになります。
1/z のポテンシャルを積分した結果は i*pi*dq、 扇形のモデルで計算した値は i*4*dq です。
この比率は次のように 円周、円の面積とそれを内接して含む四角形の外周、面積の比率のようです。
私はこの比率は面積であると思います。
扇形モデルにおける今までの結果を振り返ってみて重要な点は
- 扇形モデルでは円の半径 はキャンセルされている。
- 従って円の半径はエネルギーを計算するのに無関係である。
- 従って電荷は1点に集中しているとしても良い。
なので、1/z の積分は円の半径によらずエネルギーが計算できる扇形モデルと Uターンモデルを実現するために必要なようです。
縦方向のポテンシャル差のエネルギーを計算するためには扇形が回転しなければならない。
その回転エネルギーを計算するために 1/z が必要です。
ところがこれが大きな問題です。
ポテンシャルというのは差を計算するものであって積分するものではない。
1/z がデルタ関数の機能を持ち積分範囲 0 のエネルギーを抜き出すとしてもなかなか納得しがたいことです。
これは一体どうゆう事でしょうか?
実はこれにはちゃんとした理由がありそうなのです。
私はこれを発見したとき大変驚き次に感動しました。
なんか、翻訳を意識しているので日本語じゃないみたいな感じ。
でも、今の時点ではこれは方針を立てている途中のものだということは知っていただきたい。
なので、厳密さある程度しか無く、主にイメージを語っているということです。
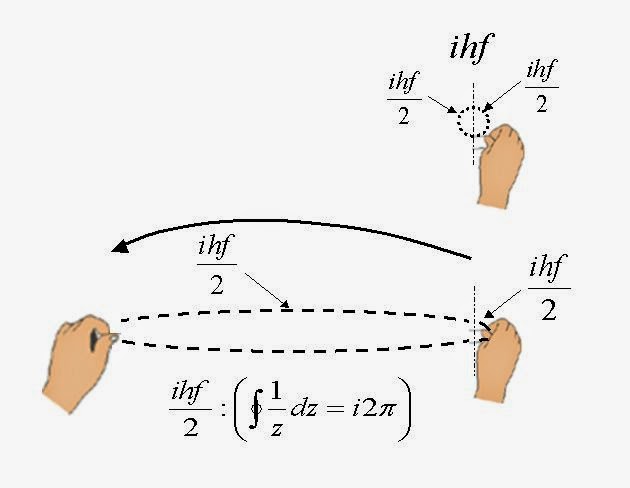
では 1/z の積分とベクトルの関係ですが。
上にある 1/z の線積分の図に補足します。
これを観て判るように結局はベクトルの内積を計算していることが判ります。
方向を示すdl ベクトルと 1/z で示されるベクトル(これの正体はなにか? 力またはポテンシャル?)は同じ方向を向いています。
従って効率100%のある値で駆動されている様子を表しています。
また、重要な点は扇形モデルで計算した結果の
値は i*4*dq ではなく i*pi*dq で計算できていることです。
さて扇形モデルで計算したエネルギーと 1/z の積分で計算したエネルギーの比率は pi/4 でした。
これが何なのかということが問題です。
これは扇形モデルでは面積の内で次のイメージ図で示す灰色の部分のエネルギーが余分に計算されているということです。
本来、遊星モデルではこの電荷は回転エネルギーを与えられて遊星運動をしています。
すると中心対称でないこの余分なエネルギーはキャンセルされるはずです。
何故かと言うと、中心対称でないと力に脈動が生じるということです。
上のイメージ図を観てわかるように灰色の部分は回転に伴って押込まれたり反発したりしてエネルギーがキャンセルされるはずです。
灰色の部分は電荷が存在するがエネルギーには関係ないようです。
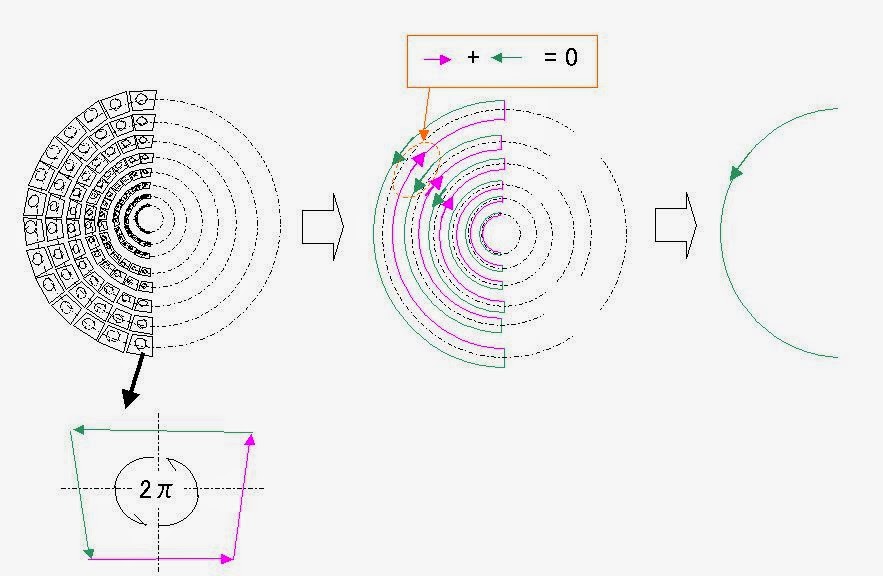
従ってこれを正しく計算するためにはこの扇形モデルで表される電荷のつまった四角形ごと回転させなければならないと思います。
この方法は簡単で、扇形モデルで方向長のベクトルと 1/z^2 で表される 力ベクトルの内積を計算してやればよい。 方向長のベクトルは遊星ギアの自転の円周を通る。
従ってグリーンの定理で示したように線積分で円周の内側だけが計算される。
つまり灰色の部分はオフされるはずだと推測しました。
-------- めも -------この部分はもう少しイメージをはっきりさせたい。
式は次のとおり、方向長ベクトルは微分したときに絶対値が同じで方向が遊星ギアにかかる力と同じ方向になるように調整してある。
または、次のとおり。
副作用として2倍の値となっているがこれは相対的な計算の影響がでているためである。
従って正確な値はこれの 1/2 と調整する必要があるはずだ。
結局、値として次の関係が成立している。
これを観ると、1/z の積分もエネルギーと等価であるとしても良いのではないだろうか?
次に仮想分裂法の3次元への拡張も検討する必要があるだろう。
多分回転なので積み重ねで表されるはずだ。
電子球の周りを帯のように包んだレール上を仮想分裂させることになると思う。
また複素数で計算すると電荷は計算上1点に集中させることができると思う。
ただし上下があるので計算上の代表点は2つで表されるイメージになると思う。
とりあえずこの方針で進んでみようと思う。
--------------------
2014/4/15
dq' にくわえられる力の意味はもう少しクリアにしないといけないと思う。
dq' に加えられている回転の力は dq'/z^2 の項による一定値のベクトルの値となり、これは結構大きい値になりますが、これは次に示すように考えることで説明できるのではないだろうか?
仮想分裂法では分裂によって開放された反発によるdq'に対応した大きなエネルギーは圧縮側に戻される。
このエネルギーは分裂による反発力と同じ大きさの力を生じさせ回転に伝えられる。
従って遊星ギアにかかる力というのは見方によりエネルギーを取り戻していると考えられる。
これが自身の回転エネルギーで円運動する。だから反発と同じ力の大きさでエネルギーを計算する意外には無いと思うのだけれど、なにかトリックで騙されてるような気もする。
円運動させているので加速度が生じてそれが力になって表されているのだろうか?
どうやら、ここで破綻したような気がします。
このテーマは変に辻褄があうので面白いんだけどあまりに続くので少し疲れてきた。
なので、今までの記事から ihf との関係をクリアにできると思うのでここに整理してとりあえずの一区切りにしよう。
--------------------
2014/4/16
えーと。
力の話はややこしいので整理すると。
- 遊星ギアの受ける自転の回転力は 1/z^2 である。
- ところがこれにより遊星ギアが公転するエネルギーを計算するのに使用する力は 1/zである。
- どちらも複素数積分するとベクトルの内積演算となる。
- 従って、通常のベクトル演算でも遊星ギアモデルであれば計算できる。
- 1/z の積分は遊星ギアの扇形モデルによる面積分の回転によるエネルギーを際外周に位置する集約した電荷でもって計算できる。 つまり集約した形式にできて簡単な取扱いができる形式になっている。
- 方向長のベクトルとの関係で 1/z はある種の力の項になっている。
で、前の記事の疑問点というのは次のことです。
- 遊星ギアの公転に与えられるエネルギーを計算するのに力 1/z は経路の全長にわたって作用している。
- この力は等ポテンシャル線にそっている。 つまり仮想電荷の力線とは直交している。
回転エネルギーを計算するのには結局のところ何かの力を使わざるを得ないのだから等ポテンシャル線にそった力を想定せざるを得ないのはしかたない。
回転だから力線に直交しないとエネルギーの収受が発生することになるので自然といえば自然であると思えます。
しかし、全長にわたって力が作用し続けるというのは何かしら直感的で無い気もする。
なのでなにか腑に落ちない感じがしています。
で仮想分裂法のイメージをもう一度観てみます。
本来分裂した場合は力線にそって反発し分裂するものを強制的に接線方向に沿って流し、それを押込みでキャンセルしています。
押込みをあたえることで回転する部分では分裂時の 1/z の力を受けるだろうということです。
この不自然さは、次のような方法で説明できるかもしれません。
- 上記の Uターンモデルは真円でのみに適用できるものかもしれない。 つまり特殊事例ではないか?
- 要は分裂と押込みによる計算は経路上の何処でも任意に想定できるかもしれない。
- また真円でなくても良い方法があるかもしれない。
- つまり真円のように綺麗な対称性のあるものでなくても良い一般的に適用できる方法があるかもしれない。
つまり、経路上の何処でもかついくらでも微細に分割でき、真円でなくても良い方法があるのかどうか? えーと一般式があるかどうかということになります。
これは何を表しているのか? ということですが、
- 電子には回転エネルギーが閉じ込められているとする。
- 電子自身は分裂方向に力がかかっているがもちろん電子は分裂などしてない。
- しかし、微視的には少し分裂してすぐに戻るということを繰り返しているのでは。
- 戻るときはポテンシャルに直交する方向に戻る。
- この戻るときに発生する力が駆動力になっている。
- 元々仮想分裂法なのでこの計算は1回(1周)のみで計算する。
- 経路が例え真円でなくても 複素数 1/z の積分であれば計算できる能力があるのかも。
という感じです。
あー、なんかすごい手間がかかりそうな気がしてきました。 まあ年単位で気長にやりましょうかねえ。 ボケ防止もかねて。 まあそんな歳です。 浮世離れした話で面白いことは面白いんですがね。
もういやになって止めちゃうかもです。 結局はしりきれトンボになりそうな気がするなあ。
--------------------
2014/4/21
遊星ギアのモデルのイメージ図だけをみると不思議な演算をしているようにみえます。
が、これは単なる線積分です。
なので不思議でもなんでもないようです。 ただ、円周方向に働くものが力であるという線積分です。
1/z の積分と 1/z^2 の積分は自然に進角で計算できるので遊星ギアのイメージにフィットしているだけのようです。
だけど、微細な部分がやはり回転で表される。
これはこれで興味深いということは言えます。
面白いといえば、あるメカニズムを想定すると 力が 1/z で表されるということです。
複素数でポテンシャルを近似(?)すると確かに極の例えば1cmも離れていればそれはポテンシャルですが極に近づくとそれは力になる。
また、半径も関係なくなる。
非常に面白い。 だけどそうなるためには電荷が均等に分布していることや円周方向に働く力を想定する等ある条件を満たす必要がありますが。
この円周方向に働く力も下のイメージ図では全周に対して働いているように思うかもしれないが表面の緑にの線だけに働いて距離を動けばあとは数学的には自然に1周することになるので 2pi で線積分しているだけです。 なのでそのエネルギーは 1/2 して補正する事になります。
・・・・・ということなのだろうか。
図を描くのに疲れたよ。 なんでこんなに時間がかかるんだろう。 ほんと底なし沼だよ。
だけど、1/z の複素数積分 はあるメカニズムを驚くほど簡潔に表すことができるというのは本当に感心する。
スーパー関数だ。
ということで、ギア比2対1の遊星ギアモデルの遊星ギアは実際には上にあるイメージ図の印象の大きさではないようです。 扇形モデルの半径方向にある微小なものである。
--------------------
2014/4/23
上の2014/4/21 の図はまったく考えが足らずに描いた図です。
なので取り消したいが、なにを書いたか判るように残しておくことにしておきます。
もう少し練りこんでから書くことにする。
とにかく、式の意味するところが多義的というか非常に味わい深いというか図にするのが非常に厄介です。
--------------------
2014/4/26
4/7の記事の最後の式ではどのような線積分をしているかというと次のようなものです。
遊星ギアのイメージとの関連は次のようになります。
これを観てみると遊星ギアのものではないのではと思われるでしょう。
しかし、積分方向を示すベクトルは一致しています。
これは進角が力が 1/z^2 なので2倍になっているためで、そのため積分長が2倍になる為です。
このような方向ベクトルの様子だけを観るとあたかも遊星ギアの運動のイメージが思い浮かびます。
ところで、そもそも何故複素数を使わなければならないのでしょうか?
今までの経緯をまとめます。
1. 1/z の積分の様子を考察していると通常のベクトルによる内積になっていることが解った。
2. そこで、複素数の積分でも通常のベクトルでの、つまり実数での積分と同じ計算ができるのではと推測。
3. それで、力を 1/z^2 とした場合、これで普通のベクトルでのエネルギー計算と同じ結果が得られる複素数の積分を探すことにしました。 ここで何故力を 1/z^2 とした理由は次のとおり。
- 1/|z^2| が 実数での力 1/r^2 と同じ。
- 1/z^2 が自然だろうと思うから。
4. その結果、この積分はある意味非常に人工的なものであるという印象があります。
それは当然で普通の実数ベクトル計算と同じになるように人為的に加工したことが原因です。
5. とにかく実数ベクトルでのエネルギー計算と同じ働きをする式が得られました。
しかし、複素数演算の結果、力を 1/z^2 としたことによる副作用として進角が2倍の項が入ってきました。
6. この2倍の進角の様子だけは遊星ギアのイメージとマッチしています。
7. その結果、1/z の積分と結果は同じであることが解りました。 ただし 1/z への式形は得られていません。 あくまでも結果が同じであるということです。
8. とにかく結果がまったく同じであるなら 1/z は等価物として用いても良いのではないかと推測します。
ということで、エネルギーを計算するのに複素数は必須というわけではありません。
しかしながら、複素数 1/zを使うメリットがあります。
- 式が極端に簡単になる。 とにかく等価物として非常に簡単な式が得られた事になる。
- 1/z はある意味力として扱える。 極の遠方ではポテンシャルの近似でもあるという面白い量に成ります。 極の近くでは虚数項が相対的に大きくなるのでここでは力と解釈できる量になります。 つまり 1/z の積分はやはりエネルギーだったかも。
- 電荷が外周の1点に集中した量として扱える。
- 直線部分でもどうやら正しく計算しているようである。 ところでエネルギーを計算するのに分裂の無限の直線を想定するのは必要ないかもしれません。 例えば人工衛星の軌道で例えると、細かく分裂し細かく落下することで円又は楕円軌道を回るわけです。 この場合も、もしも細かく分裂して細かく押込むというモデルが成立するなら1周分の計算ができることになります。 そこまで難しく考えなくても対称的なので単純に2倍するだけでも良いと思います。
- 外周の線積分の式であるということでグリーンの定理を使って連続体として扱うことができる。 4/7 の記事の式ではどうしても扇形の各微小電荷 dq' はセパレートした粒子的な感じがします。
以下は結果の値だけでの対応ですが。
このような等価関係があるといえるのでしょうか?
--------------------
2014/4/29
4/7の記事の式ですが、単位円で計算していて解りにくかったので見直した。
すると、計算が合わなくなってしまいました。
原因を探すと、次のようにしないといけないことが判った。
で、見直した結果は次のとおりになった。
ここで、やっと解ったのですが、力を 1/z^2 で計算すると積分するのはその面積分でなければいけないのではないかということです。
なので、計算を体積から計算することにした。
1/2
2/2
図の色の付いた部分はみかんの房のような形をしています。
この式は次のような表現もできます。
どうやら、球で計算しているため対称性がある為のようです。
「球の体積」 --> 「球の表面」 -->「球の円周」というように表現を縮退というか集約させることができるようです。
なので力を積分するときは面積で積分することで 積分 (1/z^2)dz^2 が成立するというわけです。
ところで、球は何次元であっても数学的に球だというのを聞いたことがあります。
このようなことは、3次元以上でも成立するのでしょうか?
しかし、計算したのはいいけれど実際的に3次元的にどんな回転してんだろ?
さっぱりイメージできないね、破綻といえばもう破綻してるなあ。
強いてイメージするとこの仮想法はボリュームでの膨張とも取れるので実際には分裂した微小部分はその地点の反対側から集まってそれぞれ半周して分裂した地点にやってくる。
それを計算するのにある軸が在るとして球の層にわけてみかんの房の形で計算する。
この房の単位で計算するのだから押込み側(球の反対側)も房の形になる。
それを仮想法でエネルギーの計算さえできればいいのだから無理やりでも仮想のレールに沿わせて軸周りの円周方向に整列させるというイメージ。
つまり仮想分裂法というより仮想膨張収縮法と言うほうが良いかもしれません。
でも、本当に軸があるのかといえば、どうでしょう、よくイメージできないんですよね。
どこといって軸なんぞあるようには思えない感じですね。 どこが軸になってもいいような。 といって定めればそれで定まるもののような不思議な感じです。
この回転は破綻していると思う。
なので最後に次のような軸周りの回転でも計算してみて、もういいかげん終わりにしたいと思う。
力は同じように半径方向の距離だけで決まるのだから同じ考えでいいと思う。
--------------------
2014/5/1
回転が軸周りであるとした場合の計算は次のようなみかんの房の表面について示せば良い。
結果は4/29の記事の計算で間違いないと思う。
ということは次のような回転ではなかったと言うことだと思う。
とはいえやはり心配なので、4/29の記事のように体積からの式を展開しておきたいと思う。
が、春の連休で帰省するのでしばらくできそうも無い。
しかし、不思議な辻褄合いはいつまで続くのだろう。 こんなことなら始めの段階で複素数の分析をしておけばよかった。
まあ、私自身、こんな話どこかで破綻するものとばかり思っていたので仕方ない。
あとわからないことは、一つ、力が円周に継続してかかり続けるものだろか?ということです。
これは微小膨張収縮で説明できるのだろうか? それしかないような気もしますが。
--------------------
2014/5/11
次
http://akimpotos.blogspot.jp/2014/05/6-complex-number-approximation-of.html