---------------------------------------------
前のページ。 Previous page
http://akimpotos.blogspot.jp/2013/07/2-complex-number-approximation-of.html
memo
クリアにすべきこと
・仮想電荷 e/2 のこと
・+∞ー∞はどこへ行ったか?
・ポテンシャルか電気力線(電界)か?
・r=0でのメカニズム詳述、密度概念とのからみ,逐次計算の様子
・ポテンシャルエネルギーの性質のこと(途中では計算できないこと・・・・)
・ポテンシャルエネルギーにおける最終構成の概念
・ポテンシャルエネルギーの性質と繰り込みの関係
・dq は dl 分で計算してよいこと
---------------------------------------------
仮想電荷 e/2について。
微小電荷を一つ一つ集合させる場合です。
仮想電荷がqです。
微小電荷間のポテンシャルエネルギーはEに含まれていません。
なのでエネルギーEの式は近似式です。
この等式はr=0の場合のみ正確なものです。
About virtual electric charge e/2.
When I let a microelectric charge gather one by one.
A virtual electric charge is q.
The potential energy between microelectric charges is not included in E.
So an expression of energy E is an approximate expression.
Only in the case of r=0, this equation is correct.
全ての電荷が一斉に集合する場合です。
この場合、仮想電荷を e/2 としています。
この場合も微小電荷間のポテンシャルエネルギーはEに含まれていません。
つまり、これも本質的に微小電荷が一つ一つ集合する場合と同じです。
なので、この場合も r = 0 以外は近似値となります。
しかし、全ての電荷が一斉に集合するイメージを描くことで見えるものがあります。
それは円周の上にあるポテンシャルと微小電荷が作るエネルギーです。
このエネルギーはr = 0 以外ではおかしな印象を与えます。
一つの微小電荷と全てのポテンシャルが作用している。 またはコンスタントであるポテンシャルが全電荷eと作用している。
しかし、全てがr=0地点で1点に集中します。
なので私はこれは r = 0 地点では自然であると考えています。
When all electric charges gather all at once.
In this case I assume a virtual electric charge e/2.
In this case the potential energy between microelectric charges is not included in E either.
In other words this is the same when a microelectric charge gathers one by one essentially.
So this case becomes the approximate value other than r = 0, too.
However, there is a thing to see by drawing the image that all electric charges gather all at once.
It is energy made with potential in the circumference and a microelectric charge.
This energy gives a funny impression any place other than r = 0.
One microelectric charge and all potential act. Or constant potential acts with all electric charge e.
However, all concentrates on one point at r=0 spot.
So I think that this is natural at the r = 0 spot.
全ての電荷を一斉に集合させるモデルは仮想電荷を e/2 としている。
結局、それは微小電荷を一つ一つ集合させるモデルと同じものです。
これは一つの方便です。
しかし、それは理解しやすいイメージを与えてくれる。
なのでこれは良い方便だと思います。
The model letting all electric charges gather all at once assumes a virtual electric charge e/2.
It is a thing same as a model letting a microelectric charge gather one by one after all.
This is one means.
However, it gives the image that it is easy to understand.
So I think that this is a good means.
なお、微小電荷間のポテンシャルエネルギーをエクセルを使って概算したところそのエネルギーは e^2/rに対し3倍以上になりました。
なので意外に大きいようです。
In addition, after roughly estimating the potential energy between microelectric charges using Excel, the energy became more than three times for e^2/r.
So it seems to be unexpectedly big.
---------------------------------------------
「無限のエネルギー」は何処にいる? Where is the infinite energy?
全ての電荷が一斉に集合する場合はもう数式には現れない。
あえて考えると次のようになる。
When all electric charges gather all at once, a formula does not show it anymore.
I am as follows when I think daringly.
不思議だ。 本当に神はいるのだろうか? そうでなければ、何故私は神の手を想定しなければいけないのか? なぜ、私はこんな不思議な仮定を置かなければ理解できないのか? なぜ、私はこんな不思議な仮定での話を大真面目に論じているのか? 考えてみれば本当に不思議なことではある。
Mysterious. Will there be really God? Otherwise why must I assume a hand of God?
Why can I not understand if I do not put such a mysterious supposition? Why do I lecture on the story in such a mysterious supposition very much seriously? It is the thing that is really mysterious if I think.
---------------------------------------------
微小電荷が一つ一つ集合する場合仮想電荷はe/2であるとされています。
r=0 の場合、正しくカーネルエネルギーを計算できます。
しかし、これは全ての電荷が一斉に集合するモデルの為の計算を適用したものです。
つまりこれは流用です。
前頁では全ての電荷が一斉に集合するモデルの場合の r=0 地点の計算方法が得られました。
微小電荷が一つ一つ集合するモデルの流用ではなく本来の仮想電荷は何でしょうか?
全ての電荷が一斉に集合するモデルの場合、本当の仮想電荷はどのようになるでしょうか?
下図のように微小電荷の塊に十分遠い所にある電荷Qに対するポテンシャルエネルギーを考えます。
すると仮想電荷はeでなければならないと思います。
When a microelectric charge gathers one by one, it is said that the virtual electric charge is e/2.
In the case of r=0, I can calculate kernel energy definitely.
However, this applied the calculation for the model whom all electric charges gathered all at once.
In other words this is diversion.
The calculation method of the r=0 spot in case of the model whom all electric charges gathered all at once was provided in the previous page.
What is the original virtual electric charge not the diversion of the model whom a microelectric charge gathers one by one?
In the case of the model whom all electric charges gather all at once, how will become the true virtual electric charge?
I think about potential energy for electric charge Q in the enough far-off place in the lump of the microelectric charge like the chart below.
Then I think the virtual electric charge to have to be e.
Mmm, I remember that this is established by "Gauss's law".
---------------------------------------------
微小電荷が一つ一つ集合するモデルの仮想電荷はe/2としていました。
現在、私はそれを見直しました。
すると仮想電荷はe/4としなければなりません。
全ての電荷が一斉に集合するモデルが正しいとすると仮想電荷はeとしなければなりません。
もしそうでないと、それは「ガウスの法則」に違反します。
つまり、微小電荷が一つ一つ集合するモデルは「ガウスの法則」に絶対的に違反します。
なぜなら数学的に等価な留数が存在するからです。
その為それは「ガウスの法則」に違反する仮想電荷を想定しなければならない。
なのでそれで正しいカーネルエネルギーを計算することは不可能です。
A microelectric charge assumed the virtual electric charge of the model who gathered one by one e/2.
I reviewed it now.
Then the virtual electric charge must assume it e/4.
If the model whom all electric charges gather all at once is right, the virtual electric charge must assume it e.
Otherwise it violates "Gauss's law".
In other words the model whom a microelectric charge gathers one by one violates "Gauss's law" absolutely.
This is because an equivalent residue exists mathematically.
Therefore it must assume a virtual electric charge to violate "Gauss's law".
So it is impossible to calculate right kernel energy in it.
---------------------------------------------
2013/9/23
中心に中心以外の対称的な構造から独立した何らかのエネルギーが存在するだろうと思います。
だけど、それがこのモデルから計算できるとは断言しません。
ただ、これは一つのトリビアとして結構面白いと思います。
飽きたのでこれで終了しよう。
I think that there will be some kind of energy independent of symmetric structure except the center in the center.
But I do not assert that I can calculate it from this model.
But I think this to be quite interesting as one trivia.
Because I got tired, I will be finished in this.
---------------------------------------------
2013/9/30
角運動量が h / (2*2*pi) となる事の推論。
思いついたので忘れないように記しておこう。
The reasoning of angular momentum becoming h / (2*2*pi).
I will write it down not to forget it because it occurred to me.
微小電荷が一つ一つ集合するモデルは以降"GOモデル"と記す。
全ての電荷が一斉に集合するモデルは以降"GAモデル"と記す。
After that I write down the model that a microelectric charge gathers one by one with "GO model ".
After that I write down the model that all electric charges gather all at once with "GA model ".
dq が中心に至る時ショックを経験する。
dqはGAモデルでは1回ショックを経験する。
これは半周に相当する。
dqが2回ショックを経験する場合、これは一周に相当する。
dq が1周すると E = h*f となる。
dqが半周するときは E / 2 = h*f / 2 となる。
dq experiences a shock in the GA model once.
This is equivalent to a semicircle.
When dq two times experience a shock, this is equivalent to one round.
When dq one lap does it, it becomes E = h*f.
When dq goes half, it becomes 2 E / = h*f / 2.
角運動量の保存。
Preservation of the angular momentum.
Ek以外のエネルギーはもう与えられないのだから角運動量保存よりエネルギーの保存を優先する必要があると思う。
I think that it is necessary to give priority to preservation of the energy over conservation of angular momentum because the energy except Ek is not given anymore.
結果として角運動量保存も成立している。
As a result, the conservation of angular momentum is established, too.
連想の為に等価な r', f' を仮定する。
これを r' -> 0 としてもエネルギー保存則は成立する。
I assume equivalent r', f' for an association.
The law of the conservation of energy is established as r' -> 0 in this.
f ' はdqがhfと同じエネルギー値を持つ場合の周波数(回転数)である。
r 'is a radius when dq has an energy level same as hf.
f 'is frequency when dq has an energy level same as hf (number of revolutions).
r ’ 、f ' はよく説明されていない。
よく説明しないとこれは誤解されるかもしれない。
後で見直そう。
r ', f' are not explained well.
This may be misunderstood when I do not explain it well.
Let's review it later.
---------------------------------------------
計算してみた。 I calculated.
f ' = 4.36 * 10^-15 r ' = 9.25 * 10^4 v ' = 2.53 * 10^-9 << C
2013/9/30 に作成した図は色々間違っていた。
なのでそれを訂正した。
The figure which I made in 2013/9/30 was wrong in various ways.
So I corrected it.
---------------------------------------------
Ek を出すために dlで積分した。
つまり *2*pi*r を乗じた。
つまり私は角運動エネルギー保存を計算した。
電子は角運動量を持つ。
なので電子は当然角運動エネルギーを持っている。
I integrated it in dl to take out Ek.
In other words I multiplied *2*pi*r.
In other words I calculated angular kinetic energy preservation.
The electron has angular momentum.
So naturally the electron has angular kinetic energy.
---------------------------------------------
Ek は完全に確定している値だ。
相対的なものではなく非相対的な値だろう。
なので Ek = m*v^2 / 2 が成立するはずだ。
なので 2013/9/30 の式を見直した。
Ek is the value that I completely establish.
It will be the value that is non-relative not a relative thing.
So Ek = m*v^2 / 2 should be established.
So I reviewed an expression of 2013/9/30.
f ' = 4.36 * 10^-15 r ' = 6.54 * 10^4 v ' = 1.79 * 10^-9 << C
---------------------------------------------
もしEk は hf の1/2 しか与えられなかったとしたら。 (1/2)(pv) = ((1/2)mv)v = p 'v となるのは自然だと思う。
もしhf が与えられたら。
Ek = pv = (mv)v = p 'vとなるべきだと思う。
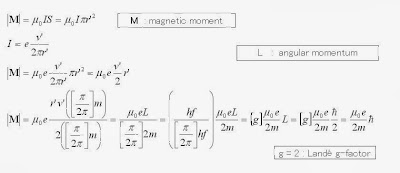
磁気モーメントについても検討してみた。
If Ek was given only 1/2 of hf. I think that it is natural to become (1/2)(pv) = ((1/2)mv)v = p 'v.
If hf is given.
I think that it should become Ek = pv = (mv)v = p 'v.
I examined the magnetic moment.
---------------------------------------------
エネルギーを整理してみた。
I classified energy.
EkQ と EQ は角運動量が異なる。 The EQ is different from EkQ in angular momentum.
---------------------------------------------
角運動量の記号をLに変更した。
I changed the sign of the angular momentum to L.
---------------------------------------------
軌道の角運動量と磁気モーメント。
Orbital angular momentum and magnetic moment.
自転と軌道の磁気モーメントは同じである。
しかし角運動量は2倍違う。
つまり自転が効率が良い。
The orbital magnetic moment is the same as the rotation.
However, the angular momentum is different in double.
In other words the rotation is efficient.
---------------------------------------------
Ekernel(Ek) が力学的でかつ量子であるということ。
Ekernel(Ek) is dynamic and being a quantum.
Ek は電子の回転エネルギーhfの半分しか与えられていないと仮定する。
つまりEk は hf/2 である。
I suppose Ek to be given only half of electron rotation energy hf.
In other words Ek is hf/2.
電子はEkを量子エネルギーとして扱う。
つまり、物質波のエネルギーとして扱う。
それでEkはpとvのみから成る。
hf は pv である。
hf = pv/2 とはならない。
ところがEk=mvv/2 である。
これは力学的エネルギーである。
仕方ないので電子はmv/2 をpとして扱う。
この結果、角運動量のみが1/2倍される。
軌道角運動量についてはこのような制限が無い。
だから1倍である。
The electron treats Ek as quantum energy.
In other words I treat it as energy of the material wave.
So Ek consists of only p and v.
hf is pv.
It does not become hf = pv/2.
However, it is Ek=mvv/2.
This is kinetic energy.
Because there is no help for it, the electron treats mv/2 as p.
As a result, only angular momentum is increased 1/2 times.
There is not such a limit about the orbital angular momentum.
Therefore it is 1 time.
要約すると。
I summarized it.
これはほとんどマジックだね。
This is almost a magic.
---------------------------------------------
以下を色々な資料で調査した。
書きやすいようにエネルギーのタイプを次のように定めた。
h/2 タイプ :kinetic - quantum
h タイプ :quantum
I investigated the following with various documents.
It determined a type of the energy as follows to be easy to write it.
h/2 type : kinetic - quantum
h type : quantum
Schrödinger 方程式は以下の前提で作られた。
この前提は2/hタイプおよびhタイプ両方において成立する。
Schrödinger equation was made with the following premises.
This premise is established in both 2/h type and h types.
「電子」の自転は h/2 タイプである。
これはパウリ方程式とDirac 方程式で証明されている。
その結果はh/2 タイプであることを示している。
The rotation of "the electron" is h/2 type.
This is proved by Pauli equation and Dirac equation.
The result shows that it is h/2 type.
http://en.wikipedia.org/wiki/Pauli_equation
「電子」の等価自転速度は v ' = 1.79 * 10^-9 << C である。
それは大変遅い。
なので非相対論的近似で成立する。
The equivalent rotation speed of "the electron" is v '= 1.79 * 10^-9 It is C.
It is very slow.
So it is established by an approximation of the non-relativism.
原子の軌道上の電子は h タイプである。
光子はh タイプである。
軌道上の電子
軌道上の角運動量は観測されている。
その結果はh タイプであることを示している。
自転の角運動量は観測されている。
その結果はh/2 タイプであることを示している。
The electron on the orbit of the atom is h type.
The photon is h type.
An electron
The angular momentum on the orbit is observed.
The result shows that it is h type.
The angular momentum of the rotation is observed.
The result shows that it is h/2 type.
では裸の「電子」はどのタイプだろうか?(自転ではない)
つまり「電子」自体の物質波のことである。
私は h/2 タイプと予想する。
もしそうなら。
物質中の電子がhタイプである事が特殊であるということに成る。
これは電子を回転させる実験で判定できると思う。
暇なときにこれに関する何らかの資料を探したい。
Then which type the naked "electron" is (not the rotation)
In other words it is a material wave of the "electron" own body.
I expect it with h/2 type.
If it is so.
It is special that an electron of materials is h type.
I think that I can judge this by an experiment to turn an electron.
When I am free, I want to look for some kind of documents about this.
---------------------------------------------
2013/10/13 を訂正した。 I corrected 2013/10/13.
---------------------------------------------
量子ワールドでは
Kpv = Khf の関係が普遍的に成立するという可能性はあるのか?
(K は 係数)
さすがに妄想だと思うが。
In the quantum world
Is there a possibility that relations of Kpv = Khf are established universally?
(K is a coefficient)
As is expected, I think that it is a delusion, but.
---------------------------------------------
lim d -> 0
2013/10/20
留数計算では計算があわない。
The calculation does not match by the residue calculation.
やはり私は留数が値を抜き出すメカニズムを参考にして物理的モデルを作る方法が良いと思う。
After all I think that a method to make a physical model in reference to the mechanism that a residue pulls out a value is good.
---------------------------------------------
スピンはあまり知らないのだけど。
「スピンの性質」と h/2 タイプと何か関連があるのだろうか?
スピンの2回転は1回転と等価になるらしい。
E = h(f/2) であるから、それは何か関係があるかもしれない。
I do not know the spin very much.
Will it have any relation with "the property of the spin" and h/2 type?
First of all of the spin let's study.
2 rotation of spin seems to be equivalent to one revolution.
Because it is E = h(f/2), it may have some relation.
---------------------------------------------
2013/10/20
「hyperfunction 」による方法は諦めた。
留数計算では下の方法で問題ないと思う。
I gave up the method by "hyperfunction".
I think that I do not have any problem by a method below by the residue calculation.
それは例えるとラーメンのスープのようだ。
材料がかき回されすぎている。
しかしとってもおいしいんだけどね。
深遠すぎて実感がわかない。
具体的な物理モデルにより理解した方がいいと思う。
だけど物理モデルも全てのポテンシャルと電荷が1点に集まっている。
思考の延長線上に在る為自然だと思える。
しかしこれは本当にOKだろうか?
As for "the Pauli_equation (the Dirac equation)" and the residue calculation, too mathematical.
It is like the soup of the ramen when I compare it.
Materials are ransacked too much.
However, it is very delicious.
It is too profound and does not get a real sense.
I think that it should be understood by concrete physical model.
But, as for the physical model, one point attracts all potential and electric charges.
I think that it is natural to be on the extension line of the thought.
However, is this really OK ?
---------------------------------------------
2013/10/25
微小電荷は仮想電荷の周りを物理的に1回回転する。
その場合留数計算は2回必要だ。
留数計算が1回しかないとそれは半周のエネルギーしかない。
The microelectric charge turns around a virtual electric charge once physically.
In that case, two times of residue calculations are necessary.
If there is only one time of residue calculation, it has only the energy of the semicircle.
---------------------------------------------
2013/10/26
これで留数計算と物理モデルの関係は明確にされたと思う。
I think that relations between residue calculation and a physical model was clarified now.
やっと此処までよろよろよろめきながらやってきたわけですが。
まあ、私の能力では仕方ありません。
この地点までの道程を振り返って思うことは,
まずは、
これはド・ブロイ波の示すものから導かれるものであること。
それで、これは現在の量子力学に影響を与えるものではない。
だけどトリビアとして興味深いものです。
次に、
私はあたかも草創期の量子力学に触れたような気がします。
私は人類の歴史において偉大な役割を果たした人たち(「ド・ブロイ」、「シュレディンガー」、「パウリ」、「ハイゼンベルグ」、「ボーア」、「アインシュタイン」、「dirac」、etc)を思い起こします。
私のごとき能力の低い者が偉大な人たちを身近に感じるというのは得がたい経験です。
特に「ド・ブロイ氏」は直感的天才の人のようで、
ド・ブロイ氏は(エネルギー、運動量と物質波)の間の関係を初めて示しました。
なので、これがド・ブロイ波の式に従うことから、私はこれが成立すると思います。
また物理法則として認められるには実験で証明される必要がある。
ド・ブロイ波は実験で証明されています。
つまり、私は既に予言されかつ実験で証明されたことを話しているに過ぎません。
けれども、これは本当に面白いトリビアだと思うんですよね。
At last I came over while staggering unsteadily to here.
Oh, there is no way with my ability.
Looking back on the distance to this spot, and thinking,
At first,
This being derived from the thing which the de Broglie wave shows.
So this is not a thing affecting the current quantum mechanics.
But it is interesting as trivia.
Then
I feel like having touched the quantum mechanics of the days of creation.
People (I recall "de Broglie", "Schrodinger", "Pauli", "Heisenberg", "Bohr", "Einstein", "dirac", etc).) that I played a great role in a history of the human
It is a rare experience that a person having low ability like me feels great people close.
"Mr. de Broglie" is in particular like the person of the intuitive genius,
Mr. de Broglie showed the relations between energy, a momentum and material wave for the first time.
So I think that this is established because this obeys the expression of the de Broglie wave.
In addition, it is necessary to be proved by an experiment so that it is recognized as a physical law.
The de Broglie wave is proved by an experiment.
In other words I talk about what it is already foretold and was proved by an experiment.
However, I think that this is really interesting trivia.
---------------------------------------------
2013/10/27
「電子」の公転のg因子を調べたところ、
「電子」の自転(h/2 type)が特殊であるということです。
After checking g factor of the revolution of "an electron,"
It means that the rotationof "an electron" (h/2 type) is special.
なるほど、公転のエネルギーを与えるのに制限は無い。
公転に必要なエネルギーが与えればいい。
なのでそれは自然だと思います。
There is not the limit indeed to give energy of the revolution.
The energy necessary for the revolution should give it.
So I think that it is natural.
(引用) (quotation).
http://www.moge.org/okabe/temp/quantum/node25.html
電子が、空間的にループ状に移動する (公転のような) 運動に対して、g 因子を求めると丁度 1 となる。
An electron moves in the shape of a loop spatially (it is like revolution). To movement, if a g factor is searched for, it will be exactly set to 1.
---------------------------------------------
2013/11/17
上記の記事は光子や物質波の運動量の取扱いがいい加減だ。
なので私はもう少し検討しないといけない。
簡単にするために一次元で検討する。
The article mentioned above is careless in the handling of the momentum of the photon and material wave.
So I should examine it a little more.
以前検討した弾性衝突の方式を適用する。
http://akimpotos.blogspot.jp/2012/01/blog-post_19.html
これは、微分方式。
http://akimpotos.blogspot.jp/2012/02/14.html
まずは物質波の場合。
I apply a method of the elastic collision which I examined before.
http://akimpotos.blogspot.jp/2012/01/blog-post_19.html
This is a differential calculus method.
http://akimpotos.blogspot.jp/2012/02/14.html
At first in the case of a material wave.
次は光子と粒子の衝突。
The next is a collision of a photon and the particle.
この場合は特殊相対性理論でのドップラー効果を計算する。
In this case I calculate Doppler effect in the special theory of relativity.
jp wiki ドップラー効果
http://ja.wikipedia.org/wiki/%E3%83%89%E3%83%83%E3%83%97%E3%83%A9%E3%83%BC%E5%8A%B9%E6%9E%9C
運動量はベクトルだ。
なので反射波と「電子」の角度を計算するとこれはコンプトン効果になる。
The momentum is a vector.
So this becomes the Compton effect when I calculate a reflection wave and the angle of "the electron".
以前の記事での運動量対応は (1/2)mv^2 の (1/2)の対応が間違っているような気がする。
また後で見直そう。
The momentum correspondence by the former article has a feeling that correspondence of (1/2) of (1/2)mv^2 is wrong.
Let's review it later.
---------------------------------------------
2013/11/18
運動量は解析で考えなければいけなかった。
ああ、これは物理学では単なる常識だろうねえ。
I had to think about the momentum by analysis.
Oh, this will be simple common sense in the physics.
ところで、仕事の都合でしばらく更新できないかもしれない。
webで物理学の勉強をする時間が無くなるだろう。
短くても1ヶ月程度。
長い場合は永遠に。
少し残念だが仕方ない。
変わらないものはなし。
いままで3年間数学と物理の勉強する時間があっただけでも良かったと思う。
だけどこの記事に関してはまた何かあったら書けると思う。
だけど新しい知識が得られなくなるのでそれなりのものにしかならないだろう。
まあ素人の与太話レベルの内容なのでどうでもいいのだが。
Time to study physics by web will be lost.
Even if short, it is about one month.
When long, it is forever.
It is unavoidable although it is somewhat regrettable.
What not changing is nothing.
I also regard as good that there was time for mathematics and physics to study for three years until now.
However, I think that it can write if there is something about this report again.
However, it will become appropriate since new knowledge is no longer acquired.Oh, it does not matter because it is the contents of the idle talk level of the amateur.
ああ、とにかく運動量の関係は全て再検討が必要だ。
なので此処まで読んだ方は注意してください。
Oh, anyway, all the relations of the momentum need reexamination.
So, please warn the person who read to here
私はしばらくの間又は永遠に書き直す暇が無い。
I do not have time to rewrite it for a while or forever.
---------------------------------------------
2013/11/18 - 2
不思議なことに上の記事の式は両方とも数学的には正しい。
これはどういう事なのだろうか?
左の式は微分で運動量(保存)を導き出した。
これは弾性衝突に適用できる。
例えばコンプトン効果に適用できる。
右の数式は単に代数的な対応だ。
慣性運動のような静的な状態が表わされているように思う。
例えばはずみ車のような恒常的な運動である。
運動エネルギーは増えもしないし減りもしない。
エネルギーは完全に閉じ込められている。
つまり「電子」の自転に適用できるのではないだろうか。
ここれが神の出したパズルに対する私の解釈である。
が、単に私は勉強不足のような気もする。
私は勘違いしているのだろうか?
もし今後十分な時間が取れれば初めから再勉強したいね。
Strangely, both expressions of the upper article are right mathematically.
What kind of thing is this?
The left expression arrived at a momentum (preservation) in differential calculus.
This is applicable to elastic collision.
For example, it is applied to Compton effect.
The right numerical formula is merely algebraic correspondence.
I think that a static state such as the inertial exercise is expressed.
For example, it is the constant exercise such as the flywheel.
The kinetic energy does not increase and does not decrease.
The energy is completely shut in.
In other words it may be applicable to the rotation of "the electron".
This is my interpretation of the puzzle which God gave.
But, merely I feel lacking in the study.
Will I misunderstand it?
I want to make a re-study from the beginning if enough time is produced in the future.
---------------------------------------------
2013/11/19
磁気モーメントと角運動量は難しすぎる。
諦めた。
角運動量は本質的に弾性衝突などの連立方程式を解くのに使う。
ところが磁気モーメント中の角運動量は単に半径r,質量mと速度vを持ってきたものだ。
つまりもともとの式の中に角運動量は存在しなかった。
もともとあったのは電流と面積だけだ。
つまり本質的に角運動量を含んでいないのではないかという疑問がある。
この場合、代数的な対応関係(右の式)が使われると思う。
だけど結局私の能力では理解できない世界ですね
The magnetic moment and angular momentum are too difficult.
It gave up.
Angular momentum is used to essentially solve simultaneous equations, such as an elastic collision.
However, the angular momentum in the magnetic moment only brought the radius r, the mass m, and the speed v.
That is, angular momentum did not exist in the formula from the first.
There were only current and area from the first.
That is, there is a question whether angular momentum is included in essence.
In this case, I think that an algebraic correspondence relation (right formula) is used.
However, it is the world which cannot be understood by my capability after all.
---------------------------------------------
2013/11/23
スピンの磁気モーメントに関わる運動量は外部の刺激に相互作用することは無い性質だと仮定する。
するとそれはモーメントというよりrmvに対応するある値である。
なのでこの値は代数的対応から得られると仮定する。
外部の刺激に相互作用する運動量は軌道角運動量である。
なのでこの値は弾性衝突のような保存量である運動量であると仮定する。
なお、角運動量自身は文字通り運動量なのは当然だ。
うーん、あまりに馬鹿げているだろうか?
2013/11/23
スピンの磁気モーメントに関わる運動量は外部の刺激に相互作用することは無い性質だと仮定する。
するとそれはモーメントというよりrmvに対応するある値である。
なのでこの値は代数的対応から得られると仮定する。
外部の刺激に相互作用する運動量は軌道角運動量である。
なのでこの値は弾性衝突のような保存量である運動量であると仮定する。
なお、角運動量自身は文字通り運動量なのは当然だ。
うーん、あまりに馬鹿げているだろうか?
I suppose that it is the property that the momentum about magnetic moment of the spin does not interact for outside stimulation.
Then it is a certain value corresponding to rmv rather than a moment.
So I suppose that this value is provided from algebraic correspondence.
The momentum to interact for outside stimulation is orbit angular momentum.
So I suppose that this value is the momentum that is quantity of preservation such as the elastic collision.
In addition, it is natural that angular momentum oneself is a momentum literally.
Mmm, will it be too stupid?
---------------------------------------------
2013/12/5
運動量は力積からも得られる。
この定積分の定数項はエネルギーの代数的mvではないだろうか?
運動量 = 動的運動量 + コンスタント運動量
コンスタント運動量はコンスタントなので運動方程式を解く為には使用されない。
だけど「電子」の磁気モーメントへはコンスタント運動量が適用されるはずである。
なぜならコンスタント運動量は外部の刺激に対して相互作用しない。コンスタント運動量は変化しない。
例えば、外部の磁気に対して変化するのは「電子」自身の運動エネルギーだ。
だから、「電子」の運動量が測定されると動的運動量が測定される。
The momentum is provided from an impulse.
http://en.wikipedia.org/wiki/Impulse_(physics)
May the constant term of this definite integral be algebraic mv of the energy?
Momentum = dynamic momentum + constant momentum
The constant momentum is not used to solve an kinetic equation because it is constant.
But a constant momentum should be applied to the magnetic moment of "the electron".
The constant momentum does not interact for outside stimulation. The constant momentum does not change.
For example, it is kinetic energy of the "electron" own to change for outside magnetism.
Therefore a dynamic momentum is measured when the momentum of "the electron" is measured.
なお、特殊相対性理論でも同様です。
エネルギーの等式を微分して運動量が出る。その運動量を微分して質量の等式が出る。
In addition, even the special theory of relativity is similar.
I differentiate an equation of the energy, and a momentum comes out. I differentiate the momentum, and an equation of the mass appears.
(物理)運動量保存はエネルギー保存則? その16
(physics) is the momentum preservation the law of the conservation of energy? No.16
http://akimpotos.blogspot.jp/2012/02/16.html
---------------------------------------------
2014/1/17
もし暇があったら勉強したいこと。
1. 微小電荷の回転は数学的に2*piだ。
しかし物理的には1*pi(半回転)だ。
これはスピンの性質と関係があるのだろうか?
2. 非弾性衝突の運動量を得る式。
(1/2)*m1*u1^2+(1/2)*m2*u2^2 = {(1/2)*m1*v1^2+(1/2)*m2*v2^2} + DB
DBは定数のエネルギーである。
この値は定数であれば無限大でも問題ない。
これは繰込み理論と関係あるのだろうか?
逆に無限大であっても方程式を解くのに無視できる値は定数だろうか?
非弾性衝突と運動量保存 Inelastic collision and momentum preservation
http://akimpotos.blogspot.jp/2012/09/blog-post.html
This is something to study if spare time is made.
1. The turn of the microelectric charge is 2*pi mathematically.
However, it is 1*pi physically (half-turn).
Will this be connected with the property of the spin?
2. An expression with a momentum of the inelastic collision.
(1/2)*m1*u1^2+(1/2)*m2*u2^2 = {(1/2)*m1*v1^2+(1/2)*m2*v2^2} + DB
DB is energy of the fixed number.
If this value is the fixed number, it is infinite and does not have any problem either.
Will this be connected with a renormalization theory?
On the contrary, is the negligible value the fixed number to solve an equation even if infinite?




























0 件のコメント:
コメントを投稿