If a time lag occurs in the thing in which energy was given in triplets' paradox http://akimpotos.blogspot.jp/2012/03/blog-post.html?
I further consider the meaning of this.
三つ子のパラドックスは別に双子のパラドックスというものがあって二つの宇宙船(AとBとします)しか存在しない場合はどちらに時間遅れが起こるのか?というものです。
With twins' paradox
When only two spacecrafts (referred to as A and B) exist, to which does a time lag happen?
なるほど二つしかない場合は一見完全に互いに同じに見えてパラドックスになっています。
When there are only two spacecrafts , which becomes completely symmetrical.
宇宙船Aが噴射していくとエネルギーが与えられたのはAなのでAがBに対して時間遅れが生じるとしてもよさそうに思いますがこれはもともとはじめに宇宙船AとBが静止状態からスタートして離れていくからであって例えば次のような場合はどうでしょうか?
The spacecraft A flies.
It is the spacecraft A that energy was given.
Therefore, in the spacecraft A, a time lag arises to the spacecraft B.
However, it is because the spacecraft A and the spacecraft B start and separate from the state of rest.
For example, when as follows, how is it?
「どこから来たのかわからない素性の知れない宇宙船AとBがやってきてすれ違おうとしている、この場合時間遅れの関係はどうなるのか?」
unknown spacecraft A and B are passing each other .
How about in this case?
この場合はこの二つの宇宙船からなる系の定点をすれ違ったところと定めれば確定しそうです。
この定点からAとBの速度が確定しそれぞれの時間遅れが計算できることになります。
In this case it is likely to be determined where spacecraft passed a fixed point of the system consisting of the two spacecraft.
So that each time delay can be calculated.velocity of A and B is determined from this fixed point.
三つ子のパラドックスはこの系の定点が地球であり、なので定点から離れる宇宙船のみに時間遅れはおこることになります。
In the paradox of triplets fixed point of this system is the earth,
So, the time delay will be occurs only on the spacecraft away from the fixed point.
双子のパラドックスは定点がAとBと二つにあるようです。
in the twin paradox, the fixed point is located on the B and A.
この考えであれば次のようなパラドックスも矛盾無く説明できます。
This idea can be explained without contradiction as well, such as the following paradox.
これのBからAをみた時間、空間変換は次のようになります。
これはBからAの船尾(としておきます)での時間と距離をみたものでAの船尾から移動しない場合です。
したがってAの船尾では時間ばかりが進むということになり結果BとAの時間比較ができるということになります。
Observing the A from B.
Time and space conversion is as follows.
We got the time and distance in the stern of the A.
It is the case that passengers do not move from the stern of the A.
In the stern of A, the only time advance will occur.
So, it means that I can compare the time.
(時間、空間は簡単のため1秒としてあります。 なので時間は光速のC、距離は速度となります。赤線がローレンツ変換で、その変換結果が現れる双対軸は青)
(there is the time and space as one second to simplify it.) So C is the velocity of light, the distance become the velocity time. A red line is Lorentz transformation. ) blue in the axis where the conversion result appears
結果は、Aでは時間はC/γ となりAの時間はBより遅れます。
The result is C/γ in A. The time of A is delayed from B.
ところがAからBを見た場合も対称的な関係であることから同じく遅れるということになりパラドックスに見えます。
However, it is the relations that are symmetric when We watch B from A. So it becomes the paradox.
で、次のような場合はどうなるかというと
Well, how about the following case?
A,Bは連結して地球から速度Uまで加速
Bは逆噴射して 速度0(地球と同じ)になる
B retro-fires and becomes velocity 0
Bが逆噴射した(エネルギーを速度に変えた)のだからBはAより時間が遅れる?
Because B retro-fired ( changed energy into velocity ), in B, is time delayed from A?
これは下のように定点Kから素直にA,B別々にローレンツ変換するとまったく矛盾がない場合が得られます。
When A,B does Lorentz transformation separately obediently from fixed point K, a case without contradiction is provided really.
Because the fixed point has two time when I watch a fixed point from each spaceship, it may become the contradiction. (in fact, as for the special theory of relativity that I do not think of carefully, a head really gets very tangled about this.)
定点を定めることにより全ての運動する物体の時間は定点に対して遅れる一方となります。
The time of all moving objects is delayed for a fixed point.
ところで宇宙船からは定点はどのように見えるかというと、これは定点の時間(Ct :t=1)、空間(定点なので 0)を変換(問い合わせてみること)すればよく時間はCγ(定点が進む)、距離は -uγ(遠ざかる) となります。
By the way, how may you see fixed point K from a spaceship?
You should convert time and space of fixed point K.
It becomes Cγ .
So time of fixed point K advances.
The distance becomes -uγ.
So fixed point K goes away from a spaceship.
更に定点を基準に宇宙船A,Bが互いにどう見えるかも計算します。
Aは定点から(C,u)、Bは(C,v)で運動しているのでAはBに、BはAに問い合わせてみます。
Furthermore, We start from fixed point K. And calculate how We can see spaceship A,B each other.
A moves from a fixed point in (C, u).
A refers to B.
B refers to A.
計算は簡単で、 AはBからγb(C-uv/C , -v+u)、BはAからγa(C-uv/C ,- u+v) と見えていることになります。
The calculation is easy.
We see A with γb(C-uv/C, -v+u) from B and B with γa(C-uv/C, - u+v) from A.
※ 宇宙船 A からBを観測した場合 observe B from spaceship A
時間項の比は、 Bの速度 v >= Aの速度 u とした場合 γb >= γa となるので分母をAとしたい場合はその比 γa/γb <= 1 (つまりBはAに比し時間が遅い)とします。
これで、時間の進み遅れが計算できます。
We assume v >= u.
The ratio of the time becomes γb >=γa.
When We assume a denominator A, it becomes the ratio γa/γb <= 1 .
in other words, in B, time is late in comparison with A.
Thus We can calculate a progress delay of the time.
速度は (-v+u) / (C-uv/C) となり合成速度が出ています。
The velocity becomes (-v+u) / (C-uv/C).
So We can calculate composition of velocity.
ところで、これは結局合成速度を出すことにしか他ならないということになります。
By the way, this becomes nothing but that We calculate composition of velocity after all.
今の気持ちはですね、オーマイゴッドですねえ。(少しガッカリ・・・)
ま、しかた無いので気を取り直して・・・。
The present feeling is O MY GOD. (disappointed a little.)
Oh, take heart.
さて本当にOKかどうかはどうやって検証したらいいのでしょうか?
何らかの方法でK点を知る方法はないのでしょうか?
双方の宇宙船がビーコンを出しそれを観測するという方法はどうでしょうか?
By the way, how should I have inspected whether I was really OK?
Will not there be the method to know the K-point by some kind of methods?
How about the method both spaceships give a beacon, and to observe it?
とりあえず本当に計算できるかどうか確かめてみます。
比 γa/γb または比 γb/γa および互いの宇宙船までの距離が計測できるものと仮定します。
We will check whether We can really calculate first of all.
We suppose that We can measure ratio γa/γb (or ratio γb/γa) and the distance to each other's spaceships.
検算 ※全ての^1/2 は+の絶対値
Checking * All ^1/2 is absolute value of +
ほぼ双子のパラドックスの場合、しかしこれは非対称
In the case of approximately twin paradox. However, this is asymmetry
結局、定点Kも自由に定めることができます。
なので、ある地点の体験をしたければその地点に行けば良いということになります。
なので、結局不思議なことは何もないと言うことですね?
We can determine fixed point K freely, too after all.
So it is expected that We should go to the spot if We want to experience a certain spot.
So is it to say that there is no mysterious thing after all?
結局、合成速度を導出するというのは3つの点の関係に他なりません。
It is nothing but the relations of three points to derive composition of velocity after all.
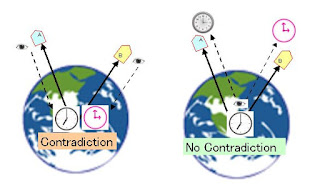
この図は3つの点の固有時間の関係を表した参考です。
値は適当に入れています。 固有時間の値の大きさの関係に矛盾はありません。
This diagram is the reference that expressed relations of the proper time of three points.
The value can come properly.
Relations of the value of the proper time do not include the contradiction.
他の定点が存在する場合も図にしてみました。
I made the diagram when other fixed points existed.
方向-速度図
direction -velocity diagram
「宇宙船が定点に向かっていくこと」と「宇宙船が定点から離れていくこと」は等価としています。
なので、矢印は外側にのみ向かいます。
なので、解釈するにはある種の癖がでるので注意が必要です。
It is equivalent that "a spaceship is separated from a fixed point" with "a spaceship going to the fixed point".
So the arrow goes outward.
So attention is necessary because a certain habit appears to interpret it.
v1による時間遅れについてですが、V0とu1による時間の遅れは同時に発生しています。
なので、全体の時間の遅れは「V0による時間の遅れ」 と 「u1による時間の遅れ」の合計 ではない。 なので矛盾は無いと思います。
About a time delay by v1, the delay of the time by V0 and u1 occurs at the same time.
So the delay of the overall time is not the total of "a delay of the time by V0" and "the delay of the time by u1".
So I think that there is not the contradiction.
念のため、u1の「固有時間」を確認しておきます。
「固有時間」はローレンツ変換の保存量で時間遅れを表します。
なので、u1のL空間中のローカル座標系でのx軸とy軸の「固有時間」を計算します。
これは、単なる合成速度を計算すればよいので、いちいち計算するまでも無く 、tu1=sqrt(1- v1^2/C^2) となります。
計算する合成速度はu1,u2のことです。念のため。
I confirm "proper time" of u1 just to make sure.
I express a delay of the time with quantity of preservation of the Lorentz transformation at "peculiar time".
So I calculate "proper time" of x-axis and the y-axis in local coordinate systems in L space of u1.
Because you should calculate simple synthetic velocity, there is not it, and this becomes tu1=sqrt(1- v1^2/C^2) even if I calculate one by one.
The composition of velocity to calculate are u1 and u2. Just to make sure.
一方、v1の「固有時間」も tv1=sqrt(1- v1^2/C^2) です。
つまり、u1の終点の時間の遅れと、v1の終点の時間の遅れは同じということになります。
u1とv1の終点は宇宙船Aです。
On the other hand, it is tv1=sqrt(1- v1^2/C^2) at "proper time" of v1.
In other words a delay of the time of the terminal of u1 and the delay of the time of the terminal of v1 are to be the same.
The terminal of u1 and v1 is spaceship A.
y軸上の「固有時間」は voy-u1y=0 なので結果 0です。
つまり、x軸上の「固有時間」だけを考慮すれば良いということになります。
Because "proper time" on the y-axis is voy-u1y=0, it is result 0.
In other words I am to consider only "proper time" on the x-axis.
この関係は、もっと極端なケースを考察すると解りやすいです。
It is easy to understand that these relations consider a more extreme case.
以上のことをとりあえず纏めます。
I settle the above-mentioned thing first of all.
1. 合成速度の関係を使ってもなお双子のパラドックスと同じパラドックスが発生する。
ある点から観測しても、また他の点から観測しても良い。
そして、それぞれで矛盾のない答えが得られる。
1. Paradox same as twin paradox still occurs even if I use the relations of the synthetic speed.
You may observe it again from other points even if you observe it from a certain point.
And an answer without the contradiction is provided in each.
2. 定点は時間遅れを比較するための基点となりうる。
2. The fixed point can become a basic point to compare the delay at time.
これを理解するための合理的な解釈は次のようなものでしょう。
1. まず、力学と時間は別のことだろう。
物体の運動やエネルギー保存に関わること、いわゆる力学では実は相対的な観測でも成立するのです。特殊相対性理論でもおなじことです。
例えば、弾性衝突の実験を飛行している宇宙船の中でしても、地球でしても同じように解くことができます。はたまた異なる宇宙船中で実験しても同じことです。
The rational interpretation to understand this will be the following thing.
1. At first, as for the time, It will be different from the mechanics.
In fact, even relative observation is established with motion of object and being concerned with energy preservation, so-called mechanics. Even the special theory of relativity is the same thing.
For example, I can untie it in the same way even if I do it in a spaceship flying an experiment of the elastic collision even if it is the earth. Or it is the same thing even if I test it in different spaceships.
参考 Reference http://akimpotos.blogspot.jp/2012_02_01_archive.html
2.例えば、宇宙線が地球に衝突する場合は力学的に宇宙線の時間が遅れてより長く進みます。
これは地球からの相対的な観測ではそうでないとエネルギー的につじつまが合わなくなるからです。
また、特殊相対性理論は観測した値を使っても良いと言っています。
しかし、ややファンシーな表現ですが宇宙線の粒子の上に小人が住んでいるとします。
この小人の年齢のとり方は力学の観測とは別の法則に従っているのではないでしょうか。
小人は地球から観測される前から宇宙線の上に住んでいるのですから・・・。
2. For example, when cosmic rays collide with the earth, the time of cosmic rays is delayed dynamically and advances for a longer time.
This is because otherwise consistency does not match energetically by the relative observation from the earth.
In addition, I say that the special theory of relativity may use the value that I observed.
However, it is slightly fancy expression, but it is said that a dwarf lives on the particle of cosmic rays.
Will not how to get age of this dwarf obey the law that is different from the observation of the mechanics?
Because the dwarf lives on cosmic rays since before was observed from the earth; :-)
3. 時間遅れの関係は下のzを定める必要があります。
定点Kが宇宙船Bにあれば時間遅れは宇宙船Aだけに発生するでしょう。
これもまた特殊相対性理論に従っていますよね?
3. It is necessary for the relations of the delay of the time to determine z.
If there is fixed point K on spaceship B, the delay of the time will occur only on spaceship A.
Does this obey the special theory of relativity again, too?
このu1,u2が判る一番簡単な例は宇宙船A,Bが交差した地点で、その地点に何か目印を置くことができればわかるでしょう。 車とちがい宇宙には地面が無いので宇宙船が交差する前には速度u1,u2は測れません。
I will understand the simplest example understanding this u1,u2 if I can put an anything mark at the spot at the spot where spaceship A,B intersected. Speed u1,u2 cannot be measured before a spaceship intersects because there is not the ground unlike a car in the space.
地球(B)から宇宙船Aが出発するということは u1=0,z=0 で交差したということと等価です。
It is equivalent with having intersected in u1=0,z=0 that spaceship A leaves earth (B).
4. 力学はもともと相対的かつ強い対称性があります。
運動体のエネルギー量は相対運動する点から観た場合容易に変化します。
4. Originally the mechanics has a relative and strong symmetry.
When I watch it from a point carrying out a relative activity, the amount of energy of the moving body changes easily.
E=m*(V+B)^2/2 B is relative velocity
一方特殊相対性理論は時間と空間の変換です。
この二つを組み合わせると相対性というより混乱が更に高まることになります。
On the other hand, the special theory of relativity is conversion of the time and space.
Confusion will rise rather than relativity more when I put these two together.
そこで私は悩むのをあきらめました。私は特殊相対性理論が示すものは無条件に認めることにします。
Therefore I gave up being troubled. I decide to recognize the thing which the special theory of relativity shows unconditionally.
つまり、矛盾していると思えることでもそれが適用できるケースが実際にあると思います。
In other words I think that there is really the case which it can apply even that I think that I contradict it to.
力学に適用する「時間」
これは完全に相対的かつ対称的な関係です。
This is completely relative and symmetric relations.
しかし、経過時間として使われることはありません。
However, there cannot be the thing used as an elapsed time.
まるでストップウォッチのようです。
This is totally like the stopwatch.
これは経過時間として使われる時間です。 これはまるで普通の時計のようです。
This is time spent as an elapsed time. This is totally like the clock.
さて、2種類の「時間」があると言うことになるのでしょうか?
By the way, will we be to have two kinds of "time" ?
再び、謎々だ?
特殊相対性理論って本当は特殊相対性謎々生成理論って言うのじゃないか?
今、なんとなくどこかの神経が切れた音が聞えたわ。
It is a riddle again?
Is the special theory of relativity that a special relative riddle generation theory actually says?
I just heard the sound that somehow some nerve was cut. :-o
冷静に考えると、やはりこのトリックはローレンツ変換の使い方の区別であるようです。
After all this trick seems to be distinction of how to use Lorentz transformation when I think calmly.
--------------------------------------------
To be continued